






3.5. Сверточные коды
Сверточные коды относятся к непрерывным кодам. Эти коды имеют большую избыточность, характеризуются простотой кодирующих устройств и наиболее пригодны для исправления пакетов ошибок.
Код образуется следующим образом. В каждый i-й тактовый момент времени на вход кодирующего устройства поступает k символов сообщения
![]()
Выходные
символы ![]() формируются с помощью рекуррентного
соотношения из К символов, поступивших на вход в данный и предшествующие
моменты времени,
формируются с помощью рекуррентного
соотношения из К символов, поступивших на вход в данный и предшествующие
моменты времени,
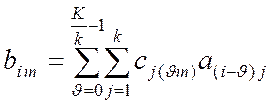 , где
, где ![]() коэффициенты
преобразования.
коэффициенты
преобразования.
Сверточными коды называют потому, что выходные символы КУ можно рассматривать как свертку импульсной характеристики КУ и входной информационной последовательности.
Величина
![]() называется
длиной кодового ограничения. Она показывает, на какое число выходных символов
влияет данный входной символ, и играет ту же роль, что и длина (разрядность)
блочного кода.
называется
длиной кодового ограничения. Она показывает, на какое число выходных символов
влияет данный входной символ, и играет ту же роль, что и длина (разрядность)
блочного кода.
Сверточный
код имеет избыточность ![]() .
.
Типичные значения: k, n = 1,2,…,8. К = 3…10. ![]() = 1/4,…,
7/8.
= 1/4,…,
7/8.
Сверточный код может быть задан несколькими способами:
1)
применением ![]() рекуррентных
соотношений, определяющих выходные символы по известным входным;
рекуррентных
соотношений, определяющих выходные символы по известным входным;
2)
с помощью производящего полинома ![]() . Степень полинома
. Степень полинома ![]() определяет число блоков выходных символов,
которые зависят от информационных.
определяет число блоков выходных символов,
которые зависят от информационных.
3) с использованием графа и кодовой решетки, а также порождающей и проверочной матриц.
Большинство эффективных сверточных кодов были получены путем перебора с помощью ЭВМ большого числа возможных кодов и выбора тех из них, которые обладали требуемыми свойствами.
Формирование сверточного кода
|
Выход |
Рассмотрим
структуру кодера на примере сверточного кода со скоростью 1/2. Сверточный
кодер с кодовым ограничением ![]() представляет собой регистр сдвига с
представляет собой регистр сдвига с ![]() ячейками. Выходные символы кодовой
последовательности образуются суммированием по модулю 2 символов с
определенным образом выбранных ячеек. На рис.3.4.1 представлен пример сверточного
кодера со скоростью 1/2. На вход кодера поступают информационные символы и для
каждого информационного символа на выходах двух сумматоров по модулю 2 формируются
два выходных символа. Связи между ячейками регистра и сумматорами можно
описать порождающими многочленами. В данном примере верхний и нижний сумматоры
описываются полиномами
ячейками. Выходные символы кодовой
последовательности образуются суммированием по модулю 2 символов с
определенным образом выбранных ячеек. На рис.3.4.1 представлен пример сверточного
кодера со скоростью 1/2. На вход кодера поступают информационные символы и для
каждого информационного символа на выходах двух сумматоров по модулю 2 формируются
два выходных символа. Связи между ячейками регистра и сумматорами можно
описать порождающими многочленами. В данном примере верхний и нижний сумматоры
описываются полиномами ![]() ,
, ![]()
Последовательность
входных символов также можно представить в виде полинома ![]() . В этом случае выходные символы сумматоров
могут быть получены умножением последовательности
. В этом случае выходные символы сумматоров
могут быть получены умножением последовательности ![]() на
порождающие полиномы. Выходная последовательность символов кодера образуется в
результате поочередного перебора с вдвое большей скоростью символов с выходов
сумматоров:
на
порождающие полиномы. Выходная последовательность символов кодера образуется в
результате поочередного перебора с вдвое большей скоростью символов с выходов
сумматоров: ![]() и
и ![]() .
Сформированная подобным образом последовательность не содержит сгруппированной
последовательности входных символов, т.е. код не является систематическим.
.
Сформированная подобным образом последовательность не содержит сгруппированной
последовательности входных символов, т.е. код не является систематическим.
Назовем
импульсной характеристикой кодера реакцию кодера на появление на входе
информационной последовательности вида 1000..., т. е. ![]() = 1. Тогда реакция кодера на
произвольную последовательность может быть представлена как результат
суммирования по модулю 2 сдвигов импульсной характеристики. Таким образом, выходная
последовательность может рассматриваться как свертка информационной
последовательности с импульсной характеристикой кодера. Соответственно,
порождающая матрица кодера может быть представлена в виде последовательности
строк, элементами которых являются соответствующим образом сдвинутые символы
импульсной характеристики. Поскольку информационная последовательность для
сверточных кодов не разбивается на блоки, и длина кодовых слов не ограничена,
порождающая матрица сверточного кода иногда называется полубесконечной.
= 1. Тогда реакция кодера на
произвольную последовательность может быть представлена как результат
суммирования по модулю 2 сдвигов импульсной характеристики. Таким образом, выходная
последовательность может рассматриваться как свертка информационной
последовательности с импульсной характеристикой кодера. Соответственно,
порождающая матрица кодера может быть представлена в виде последовательности
строк, элементами которых являются соответствующим образом сдвинутые символы
импульсной характеристики. Поскольку информационная последовательность для
сверточных кодов не разбивается на блоки, и длина кодовых слов не ограничена,
порождающая матрица сверточного кода иногда называется полубесконечной.
В нашем примере импульсная характеристика имеет вид 110111000..., порождающая матрица соответственно
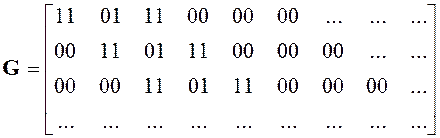
Кодовое слово, соответствующее
произвольной входной последовательности ![]() , получается в результате умножения вектора-строки
, получается в результате умножения вектора-строки ![]() на матрицу
на матрицу ![]() :
: ![]() .
.
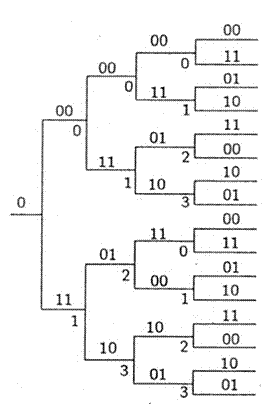
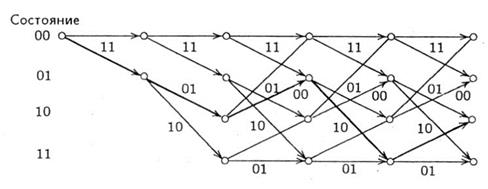
Удобно связь между входной и выходной последовательностями сверточного кодера описывать с помощью кодового дерева. При этом каждое ребро дерева отождествляется с определенным входным символом – верхнее ребро всегда с нулевым, нижнее – с единичным. Для нашего примера кодовое дерево представлено на рис.3.4.2. Каждая ветвь дерева задает выходную последовательность, соответствующую определенной входной. С ростом числа входных символов число возможных ветвей (путей) растет экспоненциально, что ограничивает практические возможности использования дерева. Можно, однако, заметить, что структура дерева сверточного кода является периодической. На рис. 5.5 каждая вершина кодового дерева обозначена числом от 0 до 3 в соответствии с содержимым двух левых ячеек кодового регистра в данной вершине дерева (младший разряд записывается левее). Это число называется состоянием кодера. Периодичность структуры дерева состоит в том, что ребра, выходящие из любых вершин, отражающих одинаковое состояние, полностью тождественны. Так, одинаковыми являются верхнее и нижнее поддеревья на уровне 3. На уровне 4 имеется четыре одинаковых куста по четыре вершины в каждом и т. д.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.