One-Variable Analysis - NORM+UNIF

One-Variable Analysis - NORM+UNIF

Analysis Summary

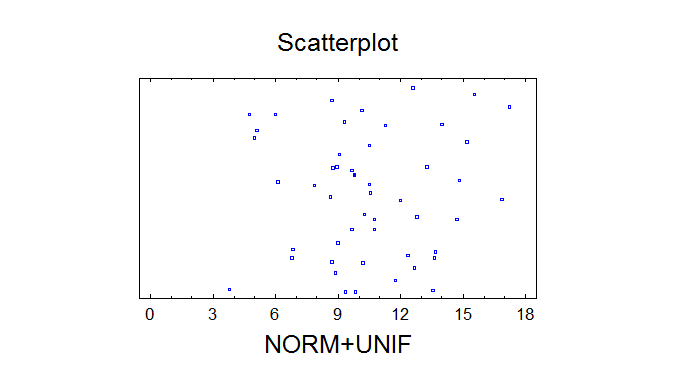
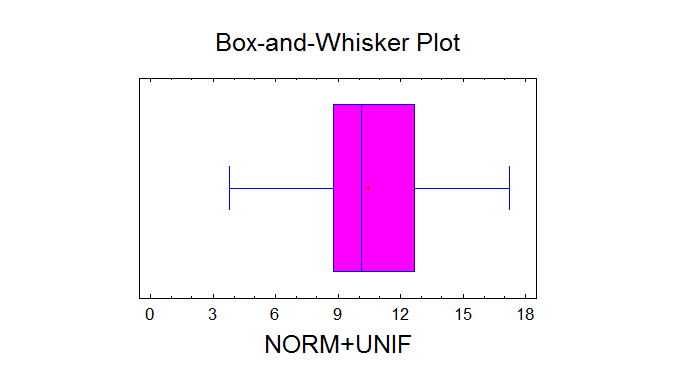
Data variable: NORM+UNIF

50 values ranging from 3,79223 to 17,2222

The StatAdvisor

--------------This procedure is designed to summarize a single sample of data.

It will calculate various statistics and graphs.  Also included in the

procedure are confidence intervals and hypothesis tests.  Use the

Tabular Options and Graphical Options buttons on the analysis toolbar

to access these different procedures.

Summary Statistics for NORM+UNIF

Count = 50

Average = 10,4379

Variance = 9,7956

Standard deviation = 3,12979

Minimum = 3,79223

Maximum = 17,2222

Range = 13,43

Stnd. skewness = 0,15692

Stnd. kurtosis = -0,37611

The StatAdvisor

--------------This table shows summary statistics for NORM+UNIF.  It includes

measures of central tendency, measures of variability, and measures of

shape.  Of particular interest here are the standardized skewness and

standardized kurtosis, which can be used to determine whether the

sample comes from a normal distribution.  Values of these statistics

outside the range of -2 to +2 indicate significant departures from

normality, which would tend to invalidate any statistical test

regarding the standard deviation.  In this case, the standardized

skewness value is within the range expected for data from a normal

distribution.  The standardized kurtosis value is within the range

expected for data from a normal distribution.

Hypothesis Tests for NORM+UNIF

Sample mean = 10,4379

Sample median = 10,1548

t-test

-----Null hypothesis: mean = 10,0

Alternative: not equal

Computed t statistic = 0,989392

P-Value = 0,327332

Do not reject the null hypothesis for alpha = 0,05.

sign test

--------Null hypothesis: median = 10,0

Alternative: not equal

Number of values below hypothesized median: 24

Number of values above hypothesized median: 26

Large sample test statistic = 0,141421 (continuity correction applied)

P-Value = 0,887532

Do not reject the null hypothesis for alpha = 0,05.

signed rank test

---------------Null hypothesis: median = 10,0

Alternative: not equal

Average rank of values below hypothesized median: 23,375

Average rank of values above hypothesized median: 27,4615

Large sample test statistic = 0,733649 (continuity correction applied)

P-Value = 0,46316

Do not reject the null hypothesis for alpha = 0,05.

The StatAdvisor

--------------This pane displays the results of three tests concerning the center

of the population from which the sample of NORM+UNIF comes.  The first

test is a t-test of the null hypothesis that the mean NORM+UNIF equals

10,0 versus the alternative hypothesis that the mean NORM+UNIF is not

equal to 10,0.  Since the P-value for this test is greater than or

equal to 0,05, we cannot reject the null hypothesis at the 95,0%

confidence level.  The second test is a sign test of the null

hypothesis that the median NORM+UNIF equals 10,0 versus the

alternative hypothesis that the median NORM+UNIF is not equal to 10,0.

It is based on counting the number of values above and below the

hypothesized median.  Since the P-value for this test is greater than

or equal to 0,05, we cannot reject the null hypothesis at the 95,0%

confidence level.  The third test is a signed rank test of the null

hypothesis that the median NORM+UNIF equals 10,0 versus the

alternative hypothesis that the median NORM+UNIF is not equal to 10,0.

It is based on comparing the average ranks of values above and below

the hypothesized median.  Since the P-value for this test is greater

than or equal to 0,05, we cannot reject the null hypothesis at the

95,0% confidence level.  The sign and signed rank tests are less

sensitive to the presence of outliers but are somewhat less powerful

than the t-test if the data all come from a single normal distribution.

Hypothesis Tests

Hypothesis Tests

---------------Sample standard deviation = 3,1735

Sample size = 50

95,0% upper confidence bound for sigma: [3,81367]

Null Hypothesis: standard deviation = 3,0

Alternative: less than

Computed chi-squared statistic = 54,8316

P-Value = 0,736951

Do not reject the null hypothesis for alpha = 0,05.

The StatAdvisor

--------------This analysis shows the results of performing a hypothesis test

concerning the standard deviation (sigma) of a normal distribution.

The two hypotheses to be tested are:

Null hypothesis:        sigma = 3,0

Alternative hypothesis: sigma < 3,0

Given a sample of 50 observations with a standard deviation of 3,1735,

the computed chi-square statistic equals 54,8316.  Since the P-value

for the test is greater than or equal to 0,05, the null hypothesis

cannot be rejected at the 95,0% confidence level.  The confidence

bound shows that the values of sigma supported by the data are less