ЦИФРОВЫЕ МЕТОДЫ СЪЕМА КООРДИНАТ ЦЕЛИ
Съем дальности.
Дискретное измерение времени запаздывания основано на заполнении этого интервала счетными импульсами, имеющими достаточно высокую и стабильную частоту повторения Fc, после чего с помощью счетчика определяется их число
![]() (1)
(1)
Схема простейшего устройства, работающего по такому принципу, изображена на рис. 1а.
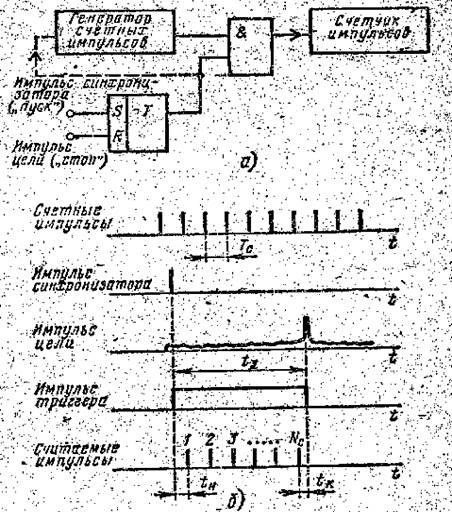
Рис.1. Съем дальности с помощью счетных импульсов
Импульс синхронизатора РЛС посредством триггера открывает каскад совпадения, через который счетные импульсы поступают на счетчик («пуск»), а импульс цели закрывает его («стоп»). Счетчик отсчитывает число импульсов за указанный промежуток времени. Так как показание дальности изменится только тогда, когда число Nc изменится, по крайней мере, на единицу, то имеет место дискретность отсчета, равная
∆Dд = c/2F
На рис. 1, б показаны временные диаграммы импульсов при несогласованном положении импульса синхронизатора и счетных импульсов. При этом
tз = (Nс - 1)Tс + tн + tк,
где tн и tк — погрешности начала и конца отсчетов.
Можно показать, что нестабильность периода повторения счетных импульсов Тс практически не влияет на погрешность. Иначе обстоит дело с погрешностями tн и tк. Также можно показать, что средняя квадратичная погрешность каждой из них можно определить по формуле
σд(D) ≈0,3∆Dд.
Для того чтобы осталась только погрешность конца отсчета, следует согласовать положение счетных импульсов и импульса синхронизатора (пунктир на рис. 1, а). Как видно из рис. 1, б, действительное расстояние всегда больше измеренного. Для того, чтобы погрешности имели разный знак, можно задержать импульс запуска передатчика на половину периода Tс/2.
Число разрядов счетчика n определяется исходя из максимальной дальности и допустимой погрешности: 2n ≥Dmах/∆Dд. Например, Dmax = 200 км и ∆D д = 20 м, 2n = 104, откуда n = 14.
Устройство, показанное на рис. 1, а, позволяет за период повторения зондирующих импульсов измерить дальность только до одной: цели, так как в момент прихода сигнального импульса цели поступление счетных импульсов на счетчик прекращается. Такое же действие может оказать помеха. Этот недостаток устраняется в схеме, показанной на рис. 2. Здесь импульс синхронизатора запускает генератор строба, который на время, равное 2Dmax/c, отпирает каскад совпадения для прохождения счетных импульсов. После окончания строба счет прекращается, и двоичный счетчик возвращается в исходное состояние. Считывание текущей дальности происходит в момент поступления импульса цели на генератор импульсов считывания. Этот генератор представляет собой комбинацию триггера и каскада совпадения. Импульсы цели проходят в счетчик на считывание лишь по окончании переходных процессов в триггерах счетчиков. Для этого импульс цели запускает триггер, импульс которого совпадает со счетными лишь после задержки в ЛЗ на время, равное длительности переходных процессов τп. Импульс на
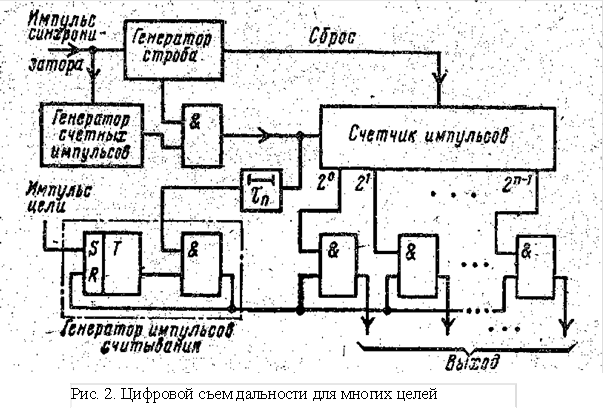 |
выходе каскада совпадения генератора импульсов считывания переводит его триггер в исходное состояние и одновременно воздействует на каскады совпадения счетчика, который выдает число, соответствующее дальности до цели. Это число в двоичном коде может поступить в блок памяти ЭВМ. При этом процесс счета не прекращается и с приходом другого импульса цели выдается другое значение дальности.
Съем углового положения цели.
Для обеспечения инструментального съема угловых координат цели целесообразно использовать цифровые методы. На рис. 3 показана структурная схема съема угловой координаты, например азимута, в РЛС кругового обзора.
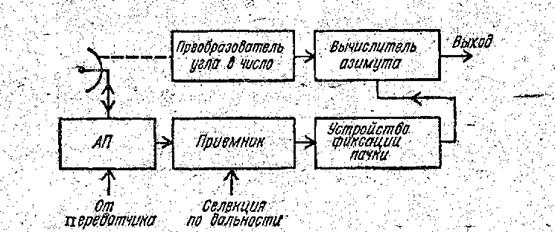
Рис. 3. Съем азимута с помощью счетных импульсов
Азимут определяется по углу поворота антенны относительно некоторого начального положения до момента прихода сигнала цели в виде пачки импульсов. В связи с этим необходимо иметь преобразователь угла поворота антенны в число, устройство фиксации положения пачки и вычислитель азимута цели. В целом такой принцип измерения не отличается от измерения дальности методом счета числа импульсов.
Рассмотрим преобразователь угла поворота антенны в двоичный код. В качестве датчиков могут использоваться электронно-оптический дисковый преобразователь, магнитный барабан, индукционные датчики и т.д. На рис. 4 показан дисковый преобразователь с прорезями.
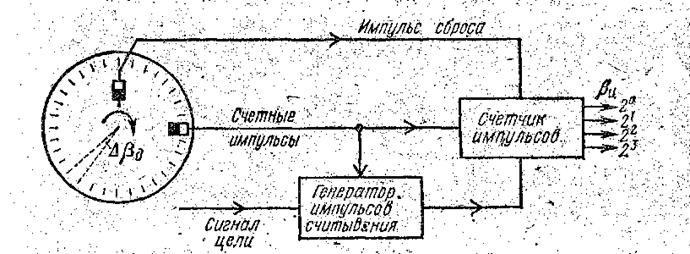
Рис.4. Преобразование угла поворота антенны в двоичный код.
По одну сторону диска размещается источник света, создающий узкий луч, засвечивающий только одну прорезь. По другую сторону диска находится фотодетектор, преобразующий световые
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.