Другие предметы \ Проектирование цифровых устройств

Синтез схемы сумматора по модулю 5

Страницы работы

19 страниц (Word-файл)
Посмотреть все страницы
Скачать файл

Фрагмент текста работы

Анализ технического задания

Необходимо синтезировать схему сумматора по модулю 5. Схема имеет 6 входов – для двух входных переменных Х1 и Х2. На выходе формируется двоичный код:

Y=(X1+X2)mod5. Сумматор имеет колличество выходов N = ]log25[ = 3

Составление таблицы истинности

Входные

коды

Значение

X1+X2

Остаток

Y

Входные

коды

Значение

X1+X2

Остаток

Y

X1

X2

X1

X2

X1

X2

X1

X2

111

111

111

111

111

111

111

111

111

110

101

100

011

010

001

000

7

7

7

7

7

7

7

7

7

6

5

4

3

2

1

0

14

13

12

11

10

9

8

7

4

3

2

1

0

4

3

2

***

***

***

***

***

***

***

***

011

011

011

011

011

011

011

011

111

110

101

100

011

010

001

000

3

3

3

3

3

3

3

3

7

6

5

4

3

2

1

0

10

9

8

7

6

5

4

3

0

4

3

2

1

0

4

3

***

***

***

010

001

000

100

011

110

110

110

110

110

110

110

110

111

110

101

100

011

010

001

000

6

6

6

6

6

6

6

6

7

6

5

4

3

2

1

0

13

12

11

10

9

8

7

6

3

2

1

0

4

3

2

1

***

***

***

***

***

***

***

***

010

010

010

010

010

010

010

010

111

110

101

100

011

010

001

000

2

2

2

2

2

2

2

2

7

6

5

4

3

2

1

0

9

8

7

6

5

4

3

2

4

3

2

1

0

4

3

2

***

***

***

001

000

100

011

010

101

101

101

101

101

101

101

101

111

110

101

100

011

010

001

000

5

5

5

5

5

5

5

5

7

6

5

4

3

2

1

0

12

11

10

9

8

7

6

5

2

1

0

4

3

2

1

0

***

***

***

***

***

***

***

***

001

001

001

001

001

001

001

001

111

110

101

100

011

010

001

000

1

1

1

1

1

1

1

1

7

6

5

4

3

2

1

0

8

7

6

5

4

3

2

1

3

2

1

0

4

3

2

1

***

***

***

000

100

011

010

001

100

100

100

100

100

100

100

100

111

110

101

100

011

010

001

000

4

4

4

4

4

4

4

4

7

6

5

4

3

2

1

0

11

10

9

8

7

6

5

4

1

0

4

3

2

1

0

4

***

***

***

011

010

001

000

100

000

000

000

000

000

000

000

000

111

110

101

100

011

010

001

000

0

0

0

0

0

0

0

0

7

6

5

4

3

2

1

0

7

6

5

4

3

2

1

0

2

1

0

4

3

2

1

0

***

***

***

100

011

010

001

000

Построим карты Карно для выходов сумматора:

y1

x1

x4
 

x2

0

0

0

0

*

*

*

*

0

1

*

*

*

*

*

*

x6

x5

0

0

*

*

*

*

*

*

1

0

*

*

*

*

*

*

0

0

*

*

*

*

*

0

0

1

*

*

*

*

*

0

x6

0

0

*

*

*

*

*

0

0

0

0

1

0

*

*

1

x3

x3

y2

x1

x4
 

x2

1

1

1

0

*

*

*

*

1

0

*

*

*

*

*

*

x6

x5

0

0

*

*

*

*

*

*

0

0

*

*

*

*

*

*

1

1

*

*

*

*

*

0

1

0

*

*

*

*

*

1

x6

0

1

*

*

*

*

*

0

0

0

0

0

1

*

*

0

x3

x3

y3

x1

x4
 

x2

0

1

0

1

*

*

*

*

1

0

*

*

*

*

*

*

x6

x5

0

1

*

*

*

*

*

*

0

0

*

*

*

*

*

*

0

1

*

*

*

*

*

1

1

0

*

*

*

*

*

0

x6

1

0

*

*

*

*

*

0

0

1

0

0

1

*

*

0

x3

x3

y1 = 1456 v2356   v

           2356  v1234 v

           2356

y2 = 2356 v 2345 v

                   14     v   1256 v

           2356  v 2356 

y3 = 3456  v 234    v

                 14     v    1356  v

           2356     v   156    v

           2346    v   1236

Сложность представления – 73 оператора.

Использование замены симметричных переменных с использованием пороговых равновесных функций

Замена пороговыми функциями симметричных переменных :

                                                   

Запрещенный набор  Z1i=0,  Z2i=1

Составим новую таблицу истинности с учётом замены переменных:

X1

X2

Z1

Z2

Y

100

100

100

100

011

100

011

111

000

010

100

010

110

000

001

100

001

101

000

000

100

000

100

000

100

011

100

111

000

010

011

011

011

011

001

011

010

011

010

000

011

001

011

001

100

011

000

011

000

011

010

100

110

000

001

010

011

011

010

000

010

010

010

010

100

010

001

011

000

011

010

000

010

000

010

001

100

101

000

000

001

011

011

001

100

001

010

011

000

011

001

001

001

001

010

001

000

001

000

001

000

100

100

000

100

000

011

011

000

011

000

010

010

000

010

000

001

001

000

001

000

000

000

000

000

Заполним полученные карты Карно:

y1(z)

z1

z2
 

z3

0

*

0

0

0

*

*

0

0

*

0

1

*

*

*

*

z6

z4

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

0

*

*

*

*

*

*

*

*

z6

*

*

*

*

*

*

*

*

0

*

1

0

0

*

*

1

z5

z5

y2(z)

z1

z2
 

z3

0

*

0

1

1

*

*

0

1

*

0

0

*

*

*

*

z6

z4

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

1

*

*

*

*

*

*

*

*

z6

*

*

*

*

*

*

*

*

0

*

0

1

0

*

*

0

z5

z5
 

y3(z)

z1

z2
 

z3

1

*

0

1

0

*

*

0

0

*

1

0

*

*

*

*

z6

z4

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

1

*

*

*

*

*

*

*

*

z6

*

*

*

*

*

*

*

*

0

*

0

0

1

*

*

0

z5

z5

y1(z) =

y2(z) =

y3(z) =

Сложность представления –42 оператора.

Анализ целесообразности совместной реализации системы функций

Для анализа целесообразности совместной реализации нужно сопостивить полученные карты Карно для функций у1, у2, у3 и построить для них таблицу мощностей следующих множеств:

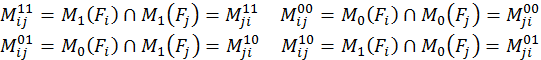
Мощность множеств

0

0

2

6

6

6

4

4

3

3

3

3

По таблице мощностей выбираем вариант связной реализации с сохранением одной из функций и сокращением нулевого характеристического подмножества второй функции.

В качестве сохранённой функции берём y1(z),  а сокращать будем нулевые характеристические подмножества y2(z) и y3(z).

Для этого сформируем функции  и  , удовлетворяющие условиям:

z1

z2
 

z3

0

*

0

1

1

*

*

0

1

*

0

*

*

*

*

*

z6

z4

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

1

*

*

*

*

*

*

*

*

z6

*

*

*

*

*

*

*

*

0

*

*

1

0

*

*

*

z5

z5

z1

z2
 

z3

1

*

0

1

0

*

*

0

0

*

1

*

*

*

*

*

z6

z4

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

1

*

*

*

*

*

*

*

*

z6

*

*

*

*

*

*

*

*

0

*

*

0

1

*

*

*

z5

z5

По сравнению с заменой симметричных переменных короче y2(z) всего на 16-13=3 оператора, а  короче y3(z) на 20-11=9 операторов. Итого суммарная сложность представления – 31 оператор.

Раздельная минимизация системы ФАЛ

Функция y1:

1)  Формируем множество простых импликант:

Запишем СКНФ функции y1(z)

Сократим СКНФ функции y1(z)

2)  Построение таблицы покрытия по результатам (AB)C:

3)  МДНФ y1(z)=

Функция

1)  Формируем множество простых импликант:

Запишем СКНФ функции

Сократим СКНФ функции

2)  Построение таблицы покрытия по результатам ABC:

3)  МДНФ

Функция

1)  Формируем множество простых импликант:

Запишем СКНФ функции

Сократим СКНФ функции

2)  Построение таблицы покрытия по результатам ABC:

3)  МДНФ

Итого суммарная сложность представления Y – 29 операторов.

Декомпозиция ФАЛ методом приближенных монотонных функций

Для функции y1(z)

Z1

Z2

Y

y1

ПМФ

ОДНФ

z1z2z3

z4z5z6

y1

f11

f21

f11

f21

123

4--

*

v

v

v

123

-5-

*

v

v

v

123

--6

*

v

v

v

12-

45-

*

v

v

v

12-

4-6

*

v

v

v

12-

-56

*

v

v

v

1-3

45-

*

v

v

v

1-3

4-6

*

v

v

v

1-3

-56

*

v

v

v

1--

456

*

v

v

v

-23

45-

*

v

v

v

-23

4-6

*

v

v

-23

-56

0

v

v

v

v

-2-

456

*

v

v

--3

456

*

123

---

0

v

v

v

v

12-

4--

*

v

v

v

12-

-5-

*

v

v

v

12-

--6

*

v

v

v

1-3

4--

*

v

v

v

1-3

-5-

*

v

v

v

1-3

--6

*

v

v

v

1--

45-

*

v

v

v

1--

4-6

*

v

v

v

1--

-56

*

v

v

-23

4--

*

-23

-5-

0

v

1

v

v

-23

--6

1

1

v

-2-

45-

*

v

v

-2-

4-6

*

-2-

-56

*

v

v

--3

45-

*

--3

4-6

*

--3

-56

*

---

456

*

12-

---

0

v

1

v

1

1-3

---

0

v

1

v

v

1--

4--

0

v

1

v

v

1--

-5-

*

v

v

1--

--6

*

v

v

-23

---

0

-2-

4--

*

-2-

-5-

1

1

v

-2-

--6

*

1

--3

4--

*

--3

-5-

*

--3

--6

0

---

45-

*

---

4-6

*

---

-56

*

1--

---

1

1

1

-2-

---

0

--3

---

0

1

---

4--

*

1

---

-5-

*

1

---

--6

*

Оптимизация y1:

Формирование множества простых импликант ПМФ f21 j=2

№

Конъюнкция

Покрываемый набор из M0

Количество покрываемых импликант

Множество импликант

1

12

-

1

+

2

13

-

1

+

3

14

-

0

-

4

15

-

0

-

5

16

-

0

-

6

23

236

2

-

7

24

-

0

-

8

26

236

0

-

9

34

-

0

-

10

35

-

1

+

11

36

236

0

-

12

45

-

0

-

13

46

-

0

-

14

56

-

0

-

Формирование множества простых импликант ПМФ f21 j=1

№

Конъюнкция

Покрываемый набор из M0

Количество покрываемых импликант

Множество импликант

1

2

25

2

-

2

3

-

3

+

3

4

-

1

+

4

5

25

0

-

5

6

-

1

+

Таблица покрытия ПМФ f21

Импликанты

12

13

14

235

3

v

v

4

v

6

12

v

Формирование множества простых импликант ПМФ f11 j=2

№

Конъюнкция

Покрываемый набор из M0

Количество покрываемых импликант

Множество импликант

1

15

-

0

-

2

16

-

0

-

3

24

-

0

-

4

26

-

1

+

5

34

-

0

-

6

35

235

0

-

7

45

-

0

-

8

46

-

0

-

9

56

-

0

-

Формирование множества простых импликант ПМФ f11 j=1

№

Конъюнкция

Покрываемый набор из M0

Количество покрываемых импликант

Множество импликант

1

4

-

0

-

2

5

-

1

+

3

6

36

0

-

Далее формирование множества простых импликант невозможно, поэтому конъюнкцию «1» заносим в таблицу покрывающих импликант

Таблица покрытия ПМФ f11

Импликанты

1

25

236

1

v

5

v

26

v

Y1=(1v5v26)*

Для функции

Z1

Z2

Y

y2

ПМФ

ОДНФ

z1z2z3

z4z5z6

y2

f11

f21

f11

f21

123

4--

*

v

v

v

v

123

-5-

*

v

v

v

v

123

--6

*

v

v

v

v

12-

45-

*

v

v

v

v

12-

4-6

*

v

v

v

v

12-

-56

*

v

v

v

v

1-3

45-

*

v

v

1-3

4-6

*

v

v

1-3

-56

*

v

v

1--

456

*

v

v

-23

45-

*

v

v

v

v

-23

4-6

*

v

v

-23

-56

0

v

v

v

v

-2-

456

*

v

v

--3

456

*

v

v

123

---

1

v

v

v

v

12-

4--

*

v

v

v

v

12-

-5-

*

v

v

v

v

12-

--6

*

v

v

v

v

1-3

4--

*

v

v

1-3

-5-

*

1-3

--6

*

v

v

1--

45-

*

v

v

1--

4-6

*

v

v

1--

-56

*

-23

4--

*

v

v

-23

-5-

0

v

1

v

v

-23

--6

*

v

v

-2-

45-

*

v

v

-2-

4-6

*

v

v

-2-

-56

*

v

v

--3

45-

*

--3

4-6

*

v

v

--3

-56

*

v

v

---

456

*

12-

---

0

v

1

v

1

1-3

---

0

1--

4--

1

1

v

1--

-5-

*

1--

--6

*

-23

---

1

v

v

-2-

4--

*

v

v

-2-

-5-

*

v

v

1

-2-

--6

*

v

v

--3

4--

*

--3

-5-

*

--3

--6

1

1

v

---

45-

*

---

4-6

*

---

-56

*

1--

---

*

-2-

---

1

1

1

--3

---

0

---

4--

*

1

---

-5-

*

---

--6

*

6

---

---

0

Оптимизация y2:

Формирование множества простых импликант ПМФ f21 j=2

№

Конъюнкция

Покрываемый набор из M0

Количество покрываемых импликант

Множество импликант

1

12

123

0

-

2

13

123

0

-

3

15

-

0

-

4

16

-

0

-

5

24

-

0

-

6

25

-

1

+

7

26

-

0

-

8

34

-

0

-

9

35

-

1

+

10

45

-

0

-

11

46

-

0

-

12

56

-

0

-

Формирование множества простых импликант ПМФ f21 j=1

№

Конъюнкция

Покрываемый набор из M0

Количество покрываемых импликант

Множество импликант

1

1

14

2

-

2

3

36, 23

1

-

3

4

14

0

-

4

5

-

0

-

5

6

36

0

-

Так как простыми импликантами j=1 не была покрыта импликанта 12, она тоже идёт в ниже приведённую таблицу

Таблица покрытия ПМФ f21

Импликанты

12

235

12

v

25

v

35

v

Формирование множества простых импликант ПМФ f11 j=1

№

Конъюнкция

Покрываемый набор из M0

Количество покрываемых импликант

Множество импликант

1

1

12

1

-

3

4

-

1

+

4

5

-

0

-

5

6

-

1

+

Далее формирование множества простых импликант невозможно, поэтому конъюнкцию «2» заносим в таблицу покрывающих импликант

Таблица покрытия ПМФ f11

Импликанты

2

14

36

2

v

4

v

6

v

Y2=(2v4v6)*)

Для функции

Z1

Z2

Y

y3

ПМФ

ОДНФ

z1z2z3

z4z5z6

y3

f11

f21

f11

f21

123

4--

*

v

v

v

123

-5-

*

v

v

v

123

--6

*

v

v

v

12-

45-

*

v

v

12-

4-6

*

v

v

12-

-56

*

v

v

1-3

45-

*

v

v

v

1-3

4-6

*

v

v

v

1-3

-56

*

v

v

v

1--

456

*

v

v

-23

45-

*

v

v

v

-23

4-6

*

v

v

v

-23

-56

1

v

v

v

-2-

456

*

--3

456

*

v

v

v

123

---

0

v

1

v

v

12-

4--

*

v

v

12-

-5-

*

v

v

12-

--6

*

v

v

1-3

4--

*

v

v

v

1-3

-5-

*

v

v

v

1-3

--6

*

v

v

v

1--

45-

*

v

v

1--

4-6

*

v

v

1--

-56

*

-23

4--

*

v

v

-23

-5-

0

v

1

v

v

-23

--6

*

v

v

v

-2-

45-

*

-2-

4-6

*

-2-

-56

*

--3

45-

*

v

v

--3

4-6

*

v

v

v

--3

-56

*

v

v

v

---

456

*

12-

---

1

1

1

1-3

---

0

v

1

v

v

1--

4--

1

1

1

1--

-5-

*

1--

--6

*

-23

---

1

v

v

-2-

4--

*

-2-

-5-

*

1

-2-

--6

*

--3

4--

*

v

v

--3

-5-

*

v

v

--3

--6

0

v

1

v

v

---

45-

*

---

4-6

*

---

-56

*

1--

---

*

-2-

---

0

--3

---

1

1

1

---

4--

*

---

-5-

*

---

--6

*

1

---

---

0

Оптимизация y3:

Формирование множества простых импликант ПМФ f21 j=2

№

Конъюнкция

Покрываемый набор из M0

Количество покрываемых импликант

Множество импликант

1

13

-

1

+

2

15

-

0

-

3

16

-

0

-

4

24

-

0

-

5

25

-

1

+

6

26

-

0

-

7

34

-

0

-

8

35

-

1

+

9

36

-

0

-

10

45

-

0

-

11

46

-

0

-

12

56

-

0

-

Формирование множества простых импликант ПМФ f21 j=1

№

Конъюнкция

Покрываемый набор из M0

Количество покрываемых импликант

Множество импликант

1

1

12

1

-

2

2

12

0

-

3

4

14

0

-

4

5

-

0

-

5

6

-

1

+

Таблица покрытия ПМФ f21

Импликанты

13

36

235

123

6

v

13

v

v

25

v

35

v

Формирование множества простых импликант ПМФ f11 j=1

№

Конъюнкция

Покрываемый набор из M0

Количество покрываемых импликант

Множество импликант

1

1

13

2

-

2

4

-

1

+

3

5

-

0

-

4

6

36

0

-

Так как простыми импликантами j=1 не были покрыты импликанты 3и 12, они тоже идут в ниже приведённую таблицу

Таблица покрытия ПМФ f11

Импликанты

3

12

14

4

v

3

v

12

v

Y3=(3v4v12)*

Выбор элементной базы

Выбор элементов определяется требованиями, заданными в ТЗ:

-напряжения питания 5в+/-5%

-Потребляемая мощность <80мвт

-время формирования выходного сигнала < 80нс.

Техно-

логия

Тип

Серия

Параметр

Рпот.,

мВт

tр..тип.,

нс

tр..макс.,

нс

Эпот.,

пДж

Глубина схемы

Сложность схемы

Б

и

п

о

л

я

р

н

ы

е

ТТЛ (Si)

быстродейств.

130

K131

22

22

6

6

10

10

132

132

8

8

10

10

ТТЛ (Si)

стандартные

K133

KM133

K155

KM155

10

10

10

10

10

10

10

10

22

22

22

22

100

100

100

100

3

3

3

4

12

12

12

12

ТТЛ (Si)

маломощные

134

1

33

100

33

1

125

ТТЛШ (Si)

быстродействующие

530

KP531

KM531

19

19

19

3

3

3

5

5

5

57

57

57

16

16

16

6

6

6

ТТЛШ (Si)

маломощные

533

K555

KM555

2

2

2

9.5

9.5

9.5

20

20

20

19

19

19

4

4

4

62

62

62

ТТЛ (Si)

быстродейст.

усовершенств.

1531

KP

1531

4

4

3

2

6

3.9

12

8

13

20

31

31

ТТЛШ (Si)

маломощные,

усовершенств.

KP

1533

1

4

11

4

7

125

ЭСЛ (Si)

100

K500

K1500

25

25

40

2

2

0.75

2.9

2.9

50

50

50

40

40

106

5

5

3

Уни-

по-

лярные

КМОП (Si)

K561

564

1564

KP

1554

0.0025 на

1МГц

0.0025 на 1

МГц

0.0025 на 1

МГц

0.0025 на 1

МГц

45

45

10

3.5

200

200

45

17

0.1

0.1

0.025

0.008

0

0

1

4

5000*

5000*

5000*

5000*

НОПТШ (GaAs)

K6500

3…6

0.1

0.42

0.3…0.6

190

13

Характеристики надёжности и сохраняемости ИС

Серия

ИС

Наработка на отказ, час

Срок

сохраняемости,

лет

КР1533

50000

15

КР1531

50000

15

1531

100000

25

КР1554

100000-125000

25

Так же надо учесть эксплуатационные требования:

-диапазон рабочих температур от -30 до +40 градусов Цельсия

-перегрузки до 5g

-одиночные удары с ускорением не более 10g, длительностью 0,1-1мкс

-вибрация с частотой 10-500 гц и ускорением не более 10g

-время наработки на отказ не менее 350000 часов

Данным требованиям удовлетворяет лишь одна серия КМОП КР1554, поэтому для дальнейшего проектирования будем использовать именно её.

Факторизация систем логических уравнений.

Уравнения выходов схемы, по результатам минимизации:

=

В данной системе уравнений можно выделить 3 конъюнктивных фактора:

Новая система уравнений выглядит так:

=

Сложность представления сократилась на 4 оператора.

Уравнения выходов схемы, по результатам декомпозиции:

Y1=(1v5v26)*

Y2=(2v4v6)*)

Y3=(3v4v12)*

F1=1v5v26 {1,2,3}

F2=3v4v12 {4,5,6}

F3=2v4v6 {7,5,8}

F4=12v25 {6,9}

F5=3v4v12 {4,5,6}

F6=6v13v25 {8,10,9}

Составим таблицу оценки качества факторов функции:

j=

Номер импликанты

Фактор

Порождающее множество

Качество

2

3,6,9,10

z1

z2

z3

z4

z5

z6

1; 6; 6; 6; 10

3; 6; 7; 6,9; 6; 9

4; 4

5; 5; 5

2; 9; 9

3; 8; 8

0

1

0

0

0

0

Выбираем  факторы:

Y1=)*

Y2=

Y3=

Разработка принципиальной схемы синтезируемого устройства.

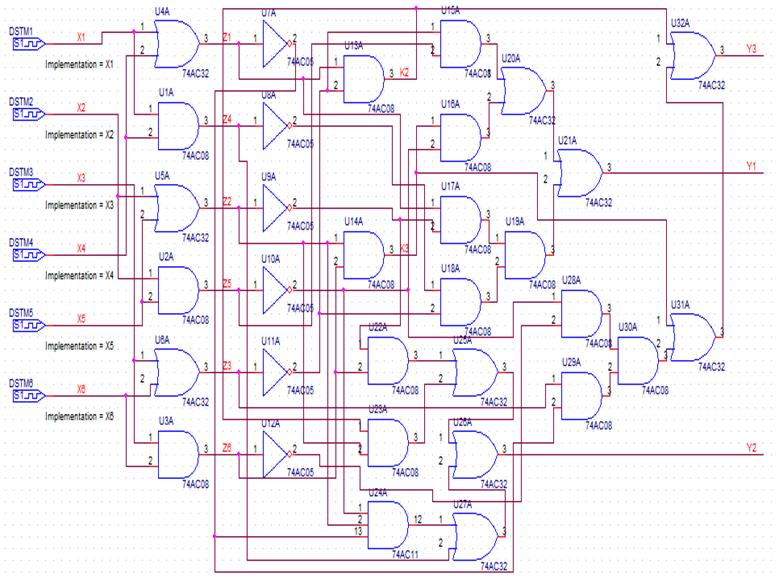
Схема, синтезированная по методу минимизации:

Тип ЛЭ

Количество ЛЭ

Тип ИС

Кол-во

ИС

Число неиспользуемых ЛЭ

h/V

3И

2И

НЕ

2ИЛИ

Буф. эл.

1

15

6

10

6

ЛИ3

ЛИ1

ЛН1

ЛЛ1

ЛП16

1

4

1

3

1

2

1

0

2

0

7/10

Тип

элемента

Обозначение

Время вкл/выкл, нс

, мкА

6хНЕ

ЛН1

6,5/7

4/40

4х2И

ЛИ1

7/7

4/40

3х3И

ЛИ3

6,5/7

4/40

4х2ИЛИ

ЛЛ1

8,5/10

4/40

Буферный элемент

ЛП16

10

4/40

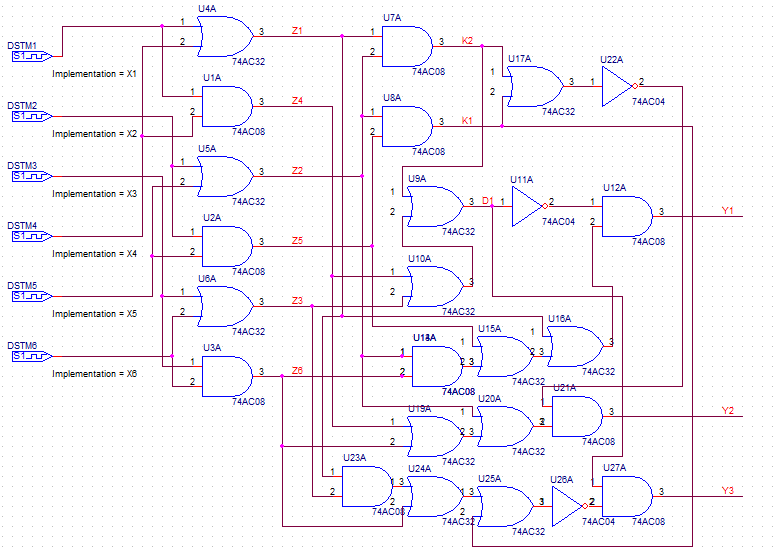
Схема, синтезированная по методу ПМФ:

Тип ЛЭ

Количество ЛЭ

Тип ИС

Кол-во

ИС

Число неиспользуемых ЛЭ

h/V

2И

НЕ

2ИЛИ

Буф. эл.

10

3

12

6

ЛИ1

ЛН1

ЛЛ1

ЛП16

3

1

3

1

2

3

0

0

7/8

Тип

элемента

Обозначение

Время вкл/выкл, нс

, мкА

6хНЕ

ЛН1

6,5/7

4/40

4х2И

ЛИ1

7/7

4/40

4х2ИЛИ

ЛЛ1

8,5/10

4/40

Буферный элемент

ЛП16

10

4/40

I1-ток при комнатной температуре, I0-максимальный ток в диапазоне рабочих температур от -45 до +85 градусов Цельсия.

Сравнив 2 схемы, и отношение h/V выбираем схему, синтезированную по методу ПМФ.

Максимальный путь распространения сигнала:

Буферный элемент-2ИЛИ-2И-2ИЛИ-2ИЛИ-НЕ-2И

Время задержки(tmax): 10+10+7+10+10+7+7=61нс

Для обеспечения помехоустойчивости по цепи питания необходимо установить развязывающие конденсаторы для защиты от низкочастотных помех суммарной емкостью не менее 15 * 0.1мкФ = 1.5мкФ , и для защиты от высокочастотных помех суммарной емкостью не менее 15*0.002мкФ=0.03мкФ . Выберем для установки на плате один конденсатор типа  мкФ, один конденсатор типа  мкФ.

В выбранном варианте реализации проектируемого устройства остаются незадействованными 2 элемента 2И и 3 элемента НЕ.

Эти элементы целесообразно использовать для повышения контролепри-годности проектируемого устройства за счёт повышения его показателей наблюдаемости. Для этого необходимо вывести на разъём через свободные логические элементы  внутренние точки схемы. Точки целесообразно выбрать в середине наиболее длинных путей распространения  сигнала от входа к выходу схемы. Поскольку суммарное количество входных, выходных шин и шин питания разрабатываемого устройства равно 10, выберем для установки на плате разъем типа ГРПМ1-32ШУ1 имеющий 16 контактов для подключения.

Расчёт основных параметров устройства.

Рассчитаем токи и мощности схемы (для расчётов используем максимальный

Похожие материалы

Информация о работе

ВУЗ:
Балтийский государственный технический университет «Военмех» имени Д. Ф. Устинова (БГТУ «Военмех»)
Предмет:
Проектирование цифровых устройств
Тип:
Курсовые работы
Категория:
Другие предметы (Технические предметы)
Размер файла:
254 Kb
Скачали:
0
Скачать файл