




































З А Д А Н И Е
на курсовое проектирование
ТЕМА: Сумматор по модулю 9 двух двоичных трехразрядных кодов
Требования:
- напряжение питания 5в +- 5%
- потребляемая мощность: не более 80 мвт
- время формирования выходного сигнала не более 100 нс
- время наработки на отказ не менее 500000 час.
Условия эксплуатации:
- диапазон рабочих температур от -300 С до +400 С;
- перегрузки до 5g;
- одиночные удары с ускорением не более 10g длительностью 0.1-1 мкс;
- вибрация с частотой 10 - 500 гц и ускорением не более 10g. .
Срок эксплуатации 15 лет, наработка за время эксплуатации до 85 тыс. часов.
Дополнительные требования.
Предусмотреть меры обеспечения контроля при изготовлении и эксплуатации
Содержание пояснительной записки.
1. Анализ технического задания
2. Составление таблицы истинности
3. Использовать замену симметричных переменных с использованием элементарных симметричных функций
4. Анализ целесообразности совместной реализации системы функций
5. Минимизация системы функций алгебры логики (раздельная)
6. Декомпозиция системы функций алгебры логики методом ПМФ
7. Выбор элементной базы
8. Факторизация системы логических уравнений
9. Разработка принципиальной схемы синтезируемого устройства
10. Расчет основных параметров устройства (время переключения, потребляемая мощность, время наработки на отказ)
11. Моделирование работы устройства, анализ правильности функционирования и состязаний в схеме.
12. Оценка степени выполнения задания
Плакаты и чертежи
1. Принципиальная схема устройства
Анализ технического задания:
Работа устройства сумматора по модулю девять описывается следующим уравнением:
![]()
![]() ,
, ![]() ,
, ![]()
Причем операнды ![]() и произведение Y удовлетворяют условию
и произведение Y удовлетворяют условию ![]()
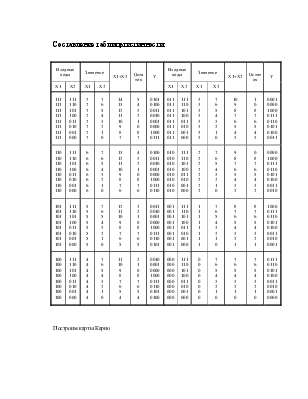
Составление таблицы истинности:
|
Входные коды |
Значение |
X1+X2 |
Остаток |
Y |
Входные коды |
Значение |
X1+X2 |
Остаток |
Y |
||||
|
X1 |
X2 |
X1 |
X2 |
X1 |
X2 |
X1 |
X2 |
||||||
|
111 111 111 111 111 111 111 111 |
111 110 101 100 011 010 001 000 |
7 7 7 7 7 7 7 7 |
7 6 5 4 3 2 1 0 |
14 13 12 11 10 9 8 7 |
5 4 3 2 1 0 8 7 |
0101 0100 0011 0010 0001 0000 1000 0111 |
011 011 011 011 011 011 011 011 |
111 110 101 100 011 010 001 000 |
3 3 3 3 3 3 3 3 |
7 6 5 4 3 2 1 0 |
10 9 8 7 6 5 4 3 |
1 0 8 7 6 5 4 3 |
0001 0000 1000 0111 0110 0101 0100 0011 |
|
110 110 110 110 110 110 110 110 |
111 110 101 100 011 010 001 000 |
6 6 6 6 6 6 6 6 |
7 6 5 4 3 2 1 0 |
13 12 11 10 9 8 7 6 |
4 3 2 1 0 8 7 6 |
0100 0011 0010 0001 0000 1000 0111 0110 |
010 010 010 010 010 010 010 010 |
111 110 101 100 011 010 001 000 |
2 2 2 2 2 2 2 2 |
7 6 5 4 3 2 1 0 |
9 8 7 6 5 4 3 2 |
0 8 7 6 5 4 3 2 |
0000 1000 0111 0110 0101 0100 0011 0010 |
|
101 101 101 101 101 101 101 101 |
111 110 101 100 011 010 001 000 |
5 5 5 5 5 5 5 5 |
7 6 5 4 3 2 1 0 |
12 11 10 9 8 7 6 5 |
3 2 1 0 8 7 6 5 |
0011 0010 0001 0000 1000 0111 0110 0101 |
001 001 001 001 001 001 001 001 |
111 110 101 100 011 010 001 000 |
1 1 1 1 1 1 1 1 |
7 6 5 4 3 2 1 0 |
8 7 6 5 4 3 2 1 |
8 7 6 5 4 3 2 1 |
1000 0111 0110 0101 0100 0011 0010 0001 |
|
100 100 100 100 100 100 100 100 |
111 110 101 100 011 010 001 000 |
4 4 4 4 4 4 4 4 |
7 6 5 4 3 2 1 0 |
11 10 9 8 7 6 5 4 |
2 1 0 8 7 6 5 4 |
0010 0001 0000 1000 0111 0110 0101 0100 |
000 000 000 000 000 000 000 000 |
111 110 101 100 011 010 001 000 |
0 0 0 0 0 0 0 0 |
7 6 5 4 3 2 1 0 |
7 6 5 4 3 2 1 0 |
7 6 5 4 3 2 1 0 |
0111 0110 0101 0100 0011 0010 0001 0000 |
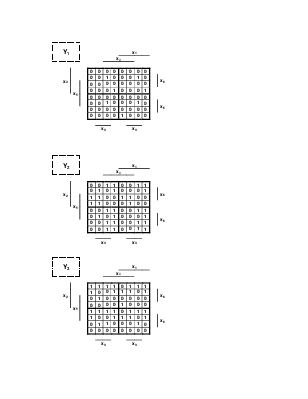
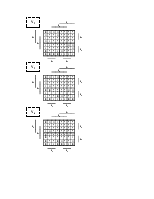
Построим карты Карно
|
Y1 |
||||||||||||||
|
x1 |
||||||||||||||
|
x4 |
||||||||||||||
|
x2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||
|
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
x6 |
||||||
|
x5 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
|
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
x6 |
||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|||||||
|
x3 |
x3 |
|||||||||||||
|
Y2 |
||||||||||||||
|
x1 |
||||||||||||||
|
x4 |
||||||||||||||
|
x2 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
||||||
|
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
x6 |
||||||
|
x5 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
||||||
|
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
|||||||
|
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|||||||
|
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
x6 |
||||||
|
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|||||||
|
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|||||||
|
x3 |
x3 |
|||||||||||||
|
Y3 |
||||||||||||||
|
x1 |
||||||||||||||
|
x4 |
||||||||||||||
|
x2 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
||||||
|
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
x6 |
||||||
|
x5 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|||||||
|
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
|||||||
|
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
x6 |
||||||
|
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
|||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
|
x3 |
x3 |
|||||||||||||
|
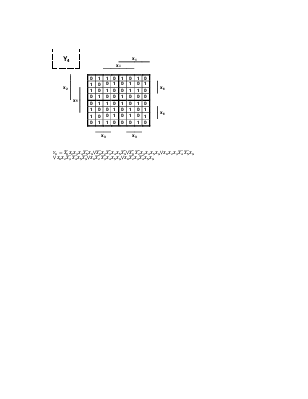
Y4 |
||||||||||||||
|
x1 |
||||||||||||||
|
x4 |
||||||||||||||
|
x2 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
||||||
|
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
x6 |
||||||
|
x5 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
||||||
|
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
|||||||
|
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
|||||||
|
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
x6 |
||||||
|
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
|||||||
|
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
|||||||
|
x3 |
x3 |
|||||||||||||
![]()
![]()
Замена симметричных переменных с использованием элементарных симметричных функций:
Симметричные переменные определим графически по картам Карно. Видно, что симметричными являются x1 и x4, x2 и x5, x3 и x6.
Произведем замену симметричных переменных:
![]()
![]()
![]()
![]()
![]()
![]()
Запрещенные наборы при этом:
![]()
![]()
![]()
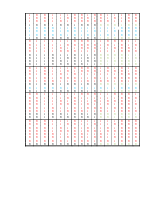
Таблица истинности с учетом симметричных переменных
|
X1 |
X2 |
Y |
Z |
||||||||||||
|
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
Y1 |
Y2 |
Y3 |
Y4 |
Z1 |
Z2 |
Z3 |
Z4 |
Z5 |
Z6 |
|
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
|
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
|
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
|
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
|
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
|
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
|
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
|
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
|
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
|
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
|
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
|
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
|
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Преобразованная таблица истинности
|
Z |
Y |
||||||||
|
Z1 |
Z2 |
Z3 |
Z4 |
Z5 |
Z6 |
Y1 |
Y2 |
Y3 |
Y4 |
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
|
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
|
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
|
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
|
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
|
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
|
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
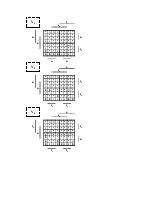
Построим карты Карно преобразованных функций:
|
Y1 |
||||||||||||||
|
z1 |
||||||||||||||
|
z2 |
||||||||||||||
|
z4 |
1 |
0 |
0 |
0 |
* |
* |
* |
* |
||||||
|
0 |
* |
* |
0 |
* |
* |
* |
* |
z6 |
||||||
|
z5 |
0 |
* |
* |
* |
* |
* |
* |
* |
||||||
|
0 |
0 |
* |
* |
* |
* |
* |
* |
|||||||
|
0 |
0 |
* |
* |
* |
* |
0 |
1 |
|||||||
|
0 |
* |
* |
* |
* |
* |
* |
0 |
z6 |
||||||
|
0 |
* |
* |
0 |
1 |
* |
* |
0 |
|||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
|
z3 |
z3 |
|||||||||||||
|
Y2 |
||||||||||||||
|
z1 |
||||||||||||||
|
z2 |
||||||||||||||
|
z4 |
0 |
0 |
0 |
0 |
* |
* |
* |
* |
||||||
|
0 |
* |
* |
0 |
* |
* |
* |
* |
z6 |
||||||
|
z5 |
1 |
* |
* |
* |
* |
* |
* |
* |
||||||
|
0 |
1 |
* |
* |
* |
* |
* |
* |
|||||||
|
1 |
1 |
* |
* |
* |
* |
0 |
0 |
|||||||
|
1 |
* |
* |
* |
* |
* |
* |
0 |
z6 |
||||||
|
0 |
* |
* |
1 |
0 |
* |
* |
1 |
|||||||
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|||||||
|
z3 |
z3 |
|||||||||||||
|
Y3 |
||||||||||||||
|
z1 |
||||||||||||||
|
z2 |
||||||||||||||
|
z4 |
0 |
0 |
1 |
0 |
* |
* |
* |
* |
||||||
|
0 |
* |
* |
1 |
* |
* |
* |
* |
z6 |
||||||
|
z5 |
0 |
* |
* |
* |
* |
* |
* |
* |
||||||
|
1 |
0 |
* |
* |
* |
* |
* |
* |
|||||||
|
0 |
0 |
* |
* |
* |
* |
0 |
0 |
|||||||
|
1 |
* |
* |
* |
* |
* |
* |
0 |
z6 |
||||||
|
1 |
* |
* |
0 |
0 |
* |
* |
1 |
|||||||
|
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
|||||||
|
z3 |
z3 |
|||||||||||||
|
Y4 |
||||||||||||||
|
z1 |
||||||||||||||
|
z2 |
||||||||||||||
|
z4 |
0 |
0 |
0 |
1 |
* |
* |
* |
* |
||||||
|
1 |
* |
* |
1 |
* |
* |
* |
* |
z6 |
||||||
|
z5 |
1 |
* |
* |
* |
* |
* |
* |
* |
||||||
|
1 |
0 |
* |
* |
* |
* |
* |
* |
|||||||
|
0 |
1 |
* |
* |
* |
* |
0 |
0 |
|||||||
|
0 |
* |
* |
* |
* |
* |
* |
1 |
z6 |
||||||
|
0 |
* |
* |
0 |
0 |
* |
* |
0 |
|||||||
|
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
|||||||
|
z3 |
z3 |
|||||||||||||
Анализ целесообразности совместной реализации системы функций:
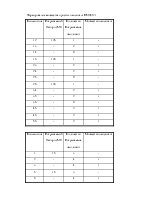
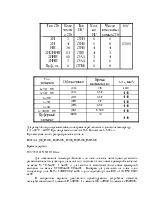
Сопоставив карты Карно функций Y1,Y2,Y3,Y4, для оценки связности функций и рассмотрения возможных способов совместной их реализации построим таблицу мощностей следующих множеств:
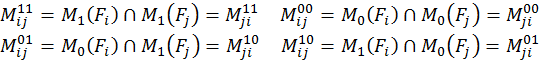
Оценка связности функций:
|
Z |
Y |
Характеристические подмножества для Y4(z), Y3(z) |
Характеристические подмножества для Y4(z), Y2(z) |
Характеристические подмножества для Y4(z), Y1(z) |
||||||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
1 |
2 |
3 |
4 |
11 |
00 |
10 |
01 |
11 |
00 |
10 |
01 |
11 |
00 |
10 |
01 |
|
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
||||||||||
|
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
|||||||||||
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
||||||||||
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
||||||||||
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
||||||||||
|
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
||||||||||
|
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
||||||||||
|
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
||||||||||
|
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
||||||||||
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
||||||||||
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
||||||||||
|
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
||||||||||
|
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
||||||||||
|
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
||||||||||
|
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
||||||||||
|
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
||||||||||
|
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
||||||||||
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
||||||||||
|
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
||||||||||
|
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
||||||||||
|
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
||||||||||
|
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
||||||||||
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
|||||||||
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
||||||||||
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
||||||||||
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
|||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
||||||||||
|
Z |
Y |
Характеристические подмножества для Y3(z), Y2(z) |
Характеристические подмножества для Y3(z), Y1(z) |
Характеристические подмножества для Y2(z), Y1(z) |
||||||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
1 |
2 |
3 |
4 |
11 |
00 |
10 |
01 |
11 |
00 |
10 |
01 |
11 |
00 |
10 |
01 |
|
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
||||||||||
|
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
||||||||||
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
||||||||||
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
||||||||||
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
||||||||||||
|
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
||||||||||
|
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
||||||||||
|
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
||||||||||
|
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
||||||||||
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
||||||||||
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
||||||||||
|
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
||||||||||
|
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|||||||||
|
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
||||||||||
|
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
||||||||||
|
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
||||||||||
|
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
||||||||||
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
||||||||||
|
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
||||||||||
|
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
|||||||||||
|
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
||||||||||
|
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
||||||||||
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
||||||||
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
||||||||||
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
||||||||||
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
|||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
||||||||||
|
Подмножество |
Мощность подмножеств |
|||||
|
|
|
|
|
|
|
|
|
|
4 |
4 |
0 |
4 |
0 |
0 |
|
|
10 |
9 |
13 |
9 |
14 |
13 |
|
|
7 |
6 |
10 |
6 |
10 |
11 |
|
|
6 |
7 |
3 |
7 |
3 |
3 |
Характеристики связности функций
Проанализировав таблицу, характеризующую связность функций, выбраем вариант связной реализации с сохранением функции у1 и сокращением нулевых характеристических подмножеств у4, у3, у2.
Для наглядности можно отобразить результат на картах Карно.
Таким образом, можно упростить реализацию системы ФАЛ.
Функция у1, останется без изменений, а нулевые наборы, сокращенные за счет реализации функции у1, будут считаться неопределенными. Каждая функция будет представляться конъюнкцией неполностью определённой функции и инверсией функции у1
|
Y1 |
||||||||||||||
|
z1 |
||||||||||||||
|
z2 |
||||||||||||||
|
z4 |
1 |
0 |
0 |
0 |
* |
* |
* |
* |
||||||
|
0 |
* |
* |
0 |
* |
* |
* |
* |
z6 |
||||||
|
z5 |
0 |
* |
* |
* |
* |
* |
* |
* |
||||||
|
0 |
0 |
* |
* |
* |
* |
* |
* |
|||||||
|
0 |
0 |
* |
* |
* |
* |
0 |
1 |
|||||||
|
0 |
* |
* |
* |
* |
* |
* |
0 |
z6 |
||||||
|
0 |
* |
* |
0 |
1 |
* |
* |
0 |
|||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
|
z3 |
z3 |
|||||||||||||
|
Y2 |
||||||||||||||
|
z1 |
||||||||||||||
|
z2 |
||||||||||||||
|
z4 |
* |
0 |
0 |
0 |
* |
* |
* |
* |
||||||
|
0 |
* |
* |
0 |
* |
* |
* |
* |
z6 |
||||||
|
z5 |
1 |
* |
* |
* |
* |
* |
* |
* |
||||||
|
0 |
1 |
* |
* |
* |
* |
* |
* |
|||||||
|
1 |
1 |
* |
* |
* |
* |
0 |
* |
|||||||
|
1 |
* |
* |
* |
* |
* |
* |
0 |
z6 |
||||||
|
0 |
* |
* |
1 |
* |
* |
* |
1 |
|||||||
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|||||||
|
z3 |
z3 |
|||||||||||||
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.