Методы конструирования РЭС и приборов

Геометрический метод конструирования

Применяется для механических конструкций, в которых должно соблюдаться точное взаимоположение и перемещение деталей.

В основу метода положена структура геометрических и кинематических связей между деталями, представляющая собой систему опорных точек, число и размещение которых зависит от числа степеней свободы и геометрических характеристик детали. Точка в пространстве имеет три степени свободы, у тела – шесть таких степеней.

Основные положения:

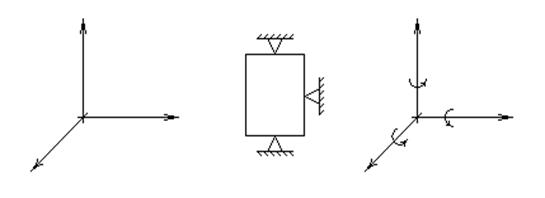
1.  Все возможные перемещения одного тела относительно другого, которые могут встречаться в системе двух конструктивно связанных тел, определяется числом и местом положения точек взаимного соприкосновения. Так как число этих точек не может превышать 6 и быть меньше единицы, то одно тело относительно другого может иметь до 5 степеней свободы.

2.  Расположение точек соприкосновения, то есть точек опоры должно быть выбрано так, чтобы каждая точка безусловно ограничивала движение тела. Если убрать эту точку, то тело получит свободу перемещения в направлении, котором ограничивалось этой точкой.

3.  Для ограничения возможного перемещения точку опоры располагают таким образом, чтобы плоскость, касательная к этой точке была перпендикулярна возможному перемещению.

4.  Чтобы сохранить с помощью точек опоры взаимное расположение тел в системе, необходимо иметь постоянно действующие силы, направленные перпендикулярно плоскостям, касательным к этим точкам. Такие силы называют замыкающими. Роль замыкающей силы может выполнять либо сила тяжести, либо сила действия специальных пружин.

Геометрический метод конструирования применяется для конструкций, в которых должно соблюдаться точное взаимное расположение отдельных деталей.

Машиностроительный метод

В основу метода положена структура механических связей между элементами в виде системы опорных поверхностей. Используется для конструирования устройств и элементов РЭС, которые несут большие механические нагрузки, в результате чего неизбежны значительные деформации.

Основные положения:

Применение опорных поверхностей вместо опорных точек.

Возможность расположения опорных поверхностей под углом к нежелательному перемещению.

Замена замыкающих сил особой формой поверхностей.

Обеспечение точности взаимного расположения деталей достигается за счёт точности их изготовления.

Топологический метод конструирования

При разработке монтажных схем, трассировки монтажа, решение задач компоновки. При этом конструкция моделируется графической структурой связей между элементами (графом) За вершины (узла) графа принимаются компоненты или их выводы, а ребрами (ветвями) являются проводники, связывающие соответствующие компоненты. Выполняя по определенным правилам преобразования графа, можно получить оптимальную конструкцию по выбранному критерию.

Задачей метода является решение задачи оптимизации размещения элементов по критерию минимума суммарной длины связей. Связность элементов определяется графом. Граф G представляет собой фигуру, состоящую из множества точек Х (вершин) и множества рёбер V (ветвей). Каждое ребро соединяет пару каких-либо вершин. Ребро называют инцидентным вершине, если оно соединяет её с другой вершиной. Граф вида G=(X,V) может быть выражен в аналитической, геометрической или матричной форме. Любые две вершины, связанные между собой ребром, называют смежными.

Основные положения:

Сопоставление связанности элементов конструкции графу.

Изоморфизм графов. У графа можно изменить порядок следования вершин при условии сохранения того же порядка соединения их инцидентными рёбрами. Преобразованный таким образом граф называют изоморфным, то есть сходным по форме с начальным графом.

Использование свойств графов для размещения элементов на печатной плате и трассировки линий связи.

При переходе от электрических схем к графам G=(X,U) для решения задач конструирования элементы схемы принимаются за вершины X=(x_i;y_j), а электрические цепи – за рёбра U=(u_i;u_j). Принципиальные электрические схемы не содержат замкнутых контуров, поэтому они отображаются плоскими графами, то есть графами с непересекающимися рёбрами. Плоскость изображается координатной сеткой, в узлах которой помещаются вершины графа.

Поиск оптимальной топологии в РЭА базируется на использовании теории графов. Поэтому представляется полезным кратко ознакомиться с ней.

*************************************************************************