
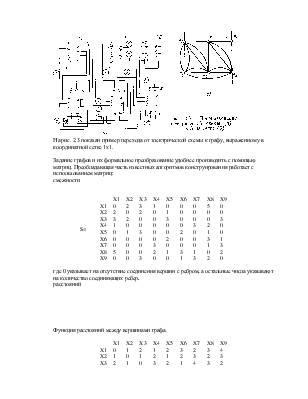

8. Переход от электрических схем к графам и матрицам.
При решении задач конструирования РЭА машинным способом используют абстрактные математические модели электрических схем и алгоритмы, легко поддающиеся программированию для реализации на ЭВМ. В наиболее приемлемом способе перехода от электрических схем к графам G= (X, U) для решения задач конструирования элементы схемы принимаются за вершины Х= {Хi, Xj), a электрические цепи — за ребра U= (Ui, Uj).
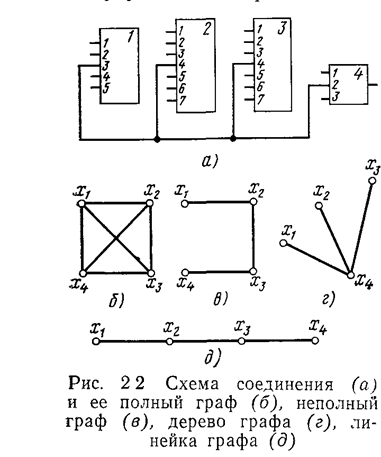
В процессе перехода от схем к графам необходимо учитывать специфику схемных элементов и предусматривать простую развязку узлов электрической цепи схемы. На рис. 2.2 показаны элементарная электрическая схема соединений из четырех элементов и возможные варианты отображения ее в граф. Как видно из рис. 2.2,6, вариант в виде полного графа имеет большое число избыточных ребер, усложняющих решение задачи, поэтому стремятся использовать более простые варианты графов, показанные на рис. 2.2,в, г, д. Также с целью упрощения задачи цепи схемы, общие для всех элементов (цепи питания, земля), при переходе к графам не учитываются.
Принципиальные электрические схемы или схемы соединений отдельных составляющих РЭА не содержат замкнутых контуров и параллельных связей, поэтому они могут быть выражены плоскими графами. Основой для прокладки' монтажных проводников служит монтажная плоскость, обычно изображаемая в виде координатной сетки. Граф, нанесенный на плоскости сетки, образует множество узлов (вершин), представляющих собой схемные элементы. Вершины графа соединяются наиболее короткими ребрами в соответствии с электрической схемой.
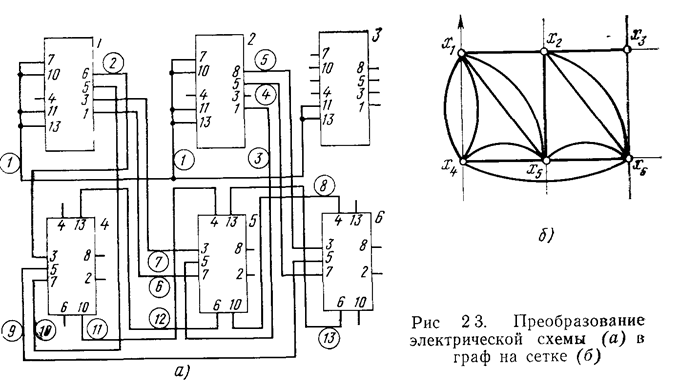
На рис. 2.3 показан пример перехода от электрической схемы к графу, выраженному в координатной сетке 1х1.
Задание графов и их формальное преобразование удобнее производить с помощью матриц. Преобладающая часть известных алгоритмов конструирования работает с использованием матриц:
смежности
|
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
X8 |
X9 |
|||
|
X1 |
0 |
2 |
3 |
1 |
0 |
0 |
0 |
5 |
0 |
||
|
X2 |
2 |
0 |
2 |
0 |
1 |
0 |
0 |
0 |
0 |
||
|
X3 |
3 |
2 |
0 |
0 |
3 |
0 |
0 |
0 |
3 |
||
|
1 |
0 |
0 |
0 |
0 |
0 |
3 |
2 |
0 |
||
|
X5 |
0 |
1 |
3 |
0 |
0 |
2 |
0 |
1 |
0 |
||
|
X6 |
0 |
0 |
0 |
0 |
2 |
0 |
0 |
3 |
1 |
||
|
X7 |
0 |
0 |
0 |
3 |
0 |
0 |
0 |
1 |
3 |
||
|
X8 |
5 |
0 |
0 |
2 |
1 |
3 |
1 |
0 |
2 |
||
|
X9 |
0 |
0 |
3 |
0 |
0 |
1 |
3 |
2 |
0 |
где 0 указывает на отсутствие соединения вершин с ребром, а остальные числа указывают на количество соединяющихребер.
расстояний
Функция расстояний между вершинами графа.
|
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
X8 |
X9 |
|||
|
X1 |
0 |
1 |
2 |
1 |
2 |
3 |
2 |
3 |
4 |
||
|
X2 |
1 |
0 |
1 |
2 |
1 |
2 |
3 |
2 |
3 |
||
|
X3 |
2 |
1 |
0 |
3 |
2 |
1 |
4 |
3 |
2 |
||
|
1 |
2 |
3 |
0 |
1 |
2 |
1 |
2 |
3 |
||
|
X5 |
2 |
1 |
2 |
1 |
0 |
1 |
2 |
1 |
2 |
||
|
X6 |
3 |
2 |
1 |
2 |
1 |
0 |
3 |
2 |
1 |
||
|
X7 |
2 |
3 |
4 |
1 |
2 |
3 |
0 |
1 |
2 |
||
|
X8 |
3 |
2 |
3 |
2 |
1 |
2 |
1 |
0 |
1 |
||
|
X9 |
4 |
3 |
2 |
3 |
2 |
1 |
2 |
1 |
0 |
Здесь число матрицы показывает количество связывающих вершины ребер наименьшей длины. Когда в графе задана длина ребер, то в матрице расстояний вместо количества ребер между рассматриваемыми вершинами удобнее указывать их суммарную длину. матрица расстояний напишется в виде
Матрица геометрии L графа, отображенного в решетке Gr, позволяет подсчитать суммарную длину его ребер. Например, матрица геометрии графа, отображенного в решетке
L=S*D=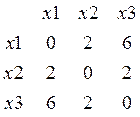 …
…
…………….
Качество трассировки печатных соединений зависит от того, насколько хорошо была решена задача размещения элементов на печатном поле. Выбирают такую числовую характеристику, которая обобщала бы все критерии (суммарная длина связи между элементами).
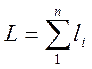
li- длина отдельного соединения;
n – общее количество.
************************************************************************
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.