Определение математического ожидания и дисперсии. Расчет вероятности попадания при каждом выстреле стрелка

Контрольные задания для студентов 2 курса (часть 2 Теория вероятностей)

10. Записать ряд распределения случайной величины

(вероятности р задать, исходя из условия: их сумма равна 1)

-----------------------------------------х    1    2     3     4      5       6

-----------------------------------------р

-------------------------------------------. 1)Найти математическое ожидание и дисперсию.2)Построить функцию распределения. 3) Найти вероятности следующих событий: случайная величина примет значение а) не больше единицы; в) не меньше своего математического ожидания.

11.Стрелок делает по мишени п выстрелов. Вероятность попадания при каждом выстреле равна р. 1)Построить ряд распределения числа попаданий. 2)Найти математическое ожидание и дисперсию числа попаданий. 3)Найти вероятность хотя бы одного попадания.Выбрать р, исходя из номера варианта

n=3;р=1)0.1;2)0,2;3)0,25;4)0,35;5)0,4;6)0,55;7)0,6;8)0,7;9)0,8;10)0,9

12. В урне имеются а белых и b черных шаров. Вынимают 2 шара.                     Построить ряд распределения числа черных шаров среди вынутых.

Найти математическое ожидание и дисперсию числа черных шаров.

12.1.а=1 b=2.12.2 а=1 b=3.12.3 а=2 b=1 12.4 а=2 b=2  12.5 а=2 b=3.

12.6 а=3 b=1.12.7 а=3 b=2 12.8 а=3 b=3 12.9 а=2 b=3. 12.10 а=1 b=4.

13.Стрелок ведет стрельбу до первого попадания, имея в запасе  n  патронов. Вероятность попадания при  одном выстреле равна р.  1)Построить ряд распределения числа израсходованных патронов.

2)Найти математическое ожидание числа израсходованных патронов.

(n,p из задачи 11)

14.Телефонная станция обслуживает n абонентов.  Вероятность того, что любой абонент позвонит в течении часа равна р. 1)Найти среднее число и дисперсию числа вызовов.2)Какова вероятность получения в течении часа от 20 до 30 вызовов?

(Использовать нормальное распределение при n=100, p из задачи 11)

.

15. Совместное распределение случайных величин задано таблицей.

1) Получить частные распределения этих величин

2) Найти М(Х), М(Y),D(X), D(Y), cov(X,Y), r .(X,Y)

315) Получить уравнения прямых регрессии Y на Х и Х на Y

4) Изобразить на плоскости возможные положения случайной точки (Х,Y). И точку ( М(Х), М(Y).Построить прямые регрессии.

Y X	y	y
.x	1/8	0
x	2/8	1/8
x	1/8	2/8
x	0	1/8

Выбрать х и y в зависимости от  номера N варианта из таблицы

N	x	x	x	x	y	y
1	0	1	2	3	-1	0
2	0	1	2	3	1	2
3	1	2	3	4	0	1
4	1	2	3	4	1	2
5	1	2	3	4	-1	0
6	-1	0	1	2	-1	0
7	-1	0	1	2	0	1
8	-1	0	1	2	1	2
9	-1	0	1	2	2	3
10	0	1	2	3	2	3

16.Найти выборочный коэффициент корреляции r и выборочное уравнение линейной регрессии y=ax+b.Построитьпрямую регрессии и изобразить на плоскости точки ( x,y) из таблицы.

16.1 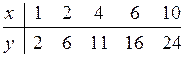        16.6

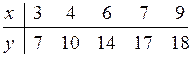
16.2 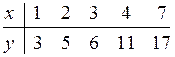                      16.7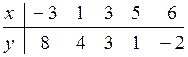    

16.3 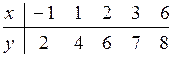                      16.8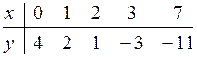    

16.4 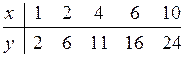                    16.9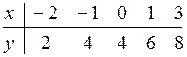   

16.5 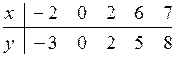                       16.10 

Методические указания

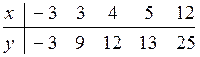
Часть 2.Теория вероятностей и математическая статистика

К этому разделу относятся задачи 10 – 16 части 2 контрольного задания

Пример 10. Задан ряд распределения случайной величины

Вероятности р заданы произвольно, исходя из условия: сумма их равна 1

-----------------------------------------х    1    2     3     4      5      6

------------------------------------------

1)Найти математическое ожидание и дисперсию.2)Построить функцию распределения. 3) Найти вероятности следующих событий: случайная величина примет значение а) не больше единицы;

в) не меньше своего математического ожидания.

Решение. 1) Здесь используются формулы для математического ожидания

М(X)= хр+хр+…хр

и дисперсии    D(X)=(х)р+(х)р+…(х)р-( М(X))

Подставляя в формулы значения из таблицы, вычислим

М(X)= 1 0,1+2 0,3+3 0,2+4 0,1+5 0,2+6 0,1=3,3

D(X)=1 0,1+4 0,3+9 0,2+16 0,1+25 0,2+36 0,1-(3,3)=2,41

2) Функция распределения F(x) равна вероятности того, что случайная величина примет значение, меньше х. Исходя из этого определения, найдем

F(x) =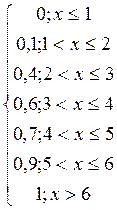

3) Р(X1)=0,1;       Р(X3,3)=0,1+0,2+0,1=0,4

Пример 11. Стрелок делает по мишени п выстрелов. Вероятность попадания при каждом выстреле равна р. 1)Построить ряд распределения числа попаданий. 2)Найти математическое ожидание и дисперсию числа попаданий. 3)Найти вероятность хотя бы одного попадания.

( n=3; р=0,3)

Решение.  При решении задачи следует использовать биномиальное распределение: P(X=m)=Cp(1-p), m=0;1;     ;n

1)Ряд распределения числа попаданий имеет вид таблицы

m     0       1       2      3 

-------------------------------р      0,343      0,441        0,189      0,027

Проверка. 0,343 + 0,441 + 0,189 + 0,027 =1

2) Среднее число или математическое ожидания и дисперсию числа попаданий  можно найти двумя способами: либо используя формулы из примера 10, или общие формулы для биномиального распределения: М(X)n p; D(X)=n p(1-p)

М(X)=3 0,3=0,9;  D(X)=3 0,3 0,7=0,633) P(X1)=1- P(X=0)=1-0,343=0,657

Пример12. В урне имеются а белых и b черных шаров. Вынимают 2 шара.                   Построить ряд распределения числа черных шаров среди вынутых.

Найти математическое ожидание и дисперсию числа черных шаров.

Решение. Пусть а=3   b=4. Очевидно, что случайное число черных шаров может принимать значения 0; 1; 2. Найдем вероятности этих значений. Обозначим через А первый вынутый шар, через В – второй вынутый шар. Индекс 1 означает, что вынутый шар – белый, индекс 2 – черный.

Р(X=0)=Р(А В)==,       Р(X=1)=Р(А В+А В)=+

+=,       Р(X=2)=Р(А В)==.

Ряд распределения числа черных шаров имеет вид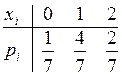          

М(X)=                 D(X)=-=

Пример 13. Стрелок ведет стрельбу до первого попадания, имея в запасе  n  патронов. Вероятность попадания при  одном выстреле равна р.  Построить ряд распределения числа израсходованных патронов.

Найти математическое ожидание числа израсходованных патронов.

(n,p из задачи 11)

Решение. n=3,  p=0,3. Очевидно, что случайное число израсходованных патронов может принимать значение 1, 2, 3. Найдем вероятности этих значений.

Обозначим А- попадание при i  выстреле, - промах при i выстреле.

Р(X=1)=Р(А)=0.3.                    Р(X=2)=Р(А)=0,7 0,3=0,21. Р(X=3)=Р()=(0,7)=0,49. Таким образом ряд распределения имеет вид

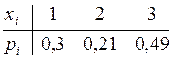
М(X)=1 0,3+2 0,21+3 0,49=2,19        D(X)=1 0,3+4 0,21+9 0,49-(2,19)=0,754

14.Телефонная станция обслуживает n абонентов.  Вероятность того, что любой абонент позвонит в течении часа равна р. Какова вероятность получения в течении часа от 20 до 30 вызовов? Найти математическое ожидание и дисперсию числа вызовов.

(Использовать нормальное распределение при n=100, p из задачи 11)

Решение. Вероятность того, что число вызовов при большом значении n будет заключено между m и m находят, используя нормальное распределение ( интегральную формулу Лапласа)

М(X)=n p=30;     D(X)=n p(1-p)=21

P(m  Xm)=Ф(х)-Ф(х),        где х=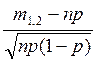, Ф(х)-интеграл вероятностей или функция Лапласа, для которой составлены таблицы