 С учетом дифракционных
минимумов большего порядка соотношение будет следующим:
С учетом дифракционных
минимумов большего порядка соотношение будет следующим: 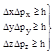 -
соотношение неопределенностей. Является следствием волновых свойств
микрочастиц.
-
соотношение неопределенностей. Является следствием волновых свойств
микрочастиц.
Соотношение неопределенностей поставили последнюю точку в споре о том, можно ли использовать законы Ньютона в микромире. Нет.
1926г. УрШредингера.
![]()
m- масса частицы.
![]()
E- полная энергия частицы.
![]() - пси-функция (волновая
функция).
- пси-функция (волновая
функция).
![]() - оператор Лапласа.
- оператор Лапласа. ![]()
С помощью![]() описывается поведение
микрочастицы в данный момент времени.
описывается поведение
микрочастицы в данный момент времени. ![]() , так
как это поведение носит вероятностный характер, то с помощью
, так
как это поведение носит вероятностный характер, то с помощью![]() надо умерь рассчитывать вероятность
обнаружения микрочастицы в данном объеме пространства. А, так как вероятность
действительная и положительная, то за меру вероятности берут не саму
надо умерь рассчитывать вероятность
обнаружения микрочастицы в данном объеме пространства. А, так как вероятность
действительная и положительная, то за меру вероятности берут не саму![]() , а квадрат ее модуля.
, а квадрат ее модуля.
![]() - плотность
вероятности (вероятность [W] обнаружения частицы в данный момент времени в единичном
объеме)
- плотность
вероятности (вероятность [W] обнаружения частицы в данный момент времени в единичном
объеме)
![]() ;
; ![]() -
вероятность достоверного события.
-
вероятность достоверного события.
Итак. Решив уравнение, получаем значение![]() ; зная ее можем рассчитать вероятность
нахождения частицы в данный момент времени в данном объеме пространства. Чтобы
; зная ее можем рассчитать вероятность
нахождения частицы в данный момент времени в данном объеме пространства. Чтобы![]() была объективной характеристикой
поведения микрочастицы, она должна обладать следующими свойствами:
была объективной характеристикой
поведения микрочастицы, она должна обладать следующими свойствами:
1. Непрерывность. Разрыв![]() может приводить к неверным результатам при
расчете вероятности.
может приводить к неверным результатам при
расчете вероятности.
2. Однозначность, чтобы не было неоднозначности при расчете вероятности.
3. Конечность, потому что вероятность не мож быть > 1.
В теории дифференциального уравнения подобного типа (2-го порядка частных производных) доказывается, что решения, удовлетворяющие свойствам непрерывности, имеют место только при определенных значениях параметра, входящего в это уравнение. Таким параметром в данном уравнении является Е (энергия микрочастицы). Следовательно, из уравнения Шредингера без каких-либо постулатов вытекает дескретный ряд значений полной энергии микрочастицы.
Применение уравнения (1) к атому H2.
![]()
Решение уравнения дает:
1. Значение энергии.![]() ; n=1,2,3…
; n=1,2,3…
2. Значение волновой функции.![]()
dV- объем, в котором находится частица.
dW- вероятность нахождения частицы в заданном объеме.
Т.к. электрон в атоме имеет три степени свободы (i=3),
то![]() является функцией трех квантовых чисел (
является функцией трех квантовых чисел (![]() ).
).
n- главное квантовое число (n=1,2,3…).
l- азимутальное (орбитальное) квантовое число (l=0,1,2,…,n-1). l принимает n различных значений.
m-
магнитное квантовое число (![]() ). m принимает
2l+1 различных значений.
). m принимает
2l+1 различных значений.
Сколько может быть различных состояний электрона с одним и тем же значением n?
![]() Не может
быть двух состояний (электронов), в которых все квантовые числа одинаковые.
Не может
быть двух состояний (электронов), в которых все квантовые числа одинаковые.
Под термином: «различные квантовые состояния» понимаются состояния, которые отличаются значение хотя бы одного квантового числа.
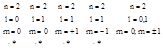 Это есть
принцип Паули для электрона в атоме (n2).
Это есть
принцип Паули для электрона в атоме (n2).
(![]() )-обозначение двух
противоположных направления собственных спиновых моментов (Mzs).
)-обозначение двух
противоположных направления собственных спиновых моментов (Mzs).
Состояние с l=0 называется s–состоянием; с l=2 называется р–состоянием; с l=3 называется d–состоянием.
Физический смысл квантовых чисел.
1. n- гл квантовое число Определяет энергию ![]() . Данн велич дискрет,
строго определ.
. Данн велич дискрет,
строго определ.
2. l- азимутальное (орбитальное) квантовое число. Определяет момент импульса на орбите (орбитальный механический момент). Определяет форму орбиты.
М![]() плоскости орбиты. Из
уравнения Шредингера следует
плоскости орбиты. Из
уравнения Шредингера следует ![]() . Данная величина
дискретная, строго определенная.
. Данная величина
дискретная, строго определенная.
3. m- магнитное квантовое число. Определяет проекцию момента импульса на ось.
Определяет ориентацию орбиты в пространстве. Mz=m![]() - дискретная величина.
Рис.1.9.
- дискретная величина.
Рис.1.9.
Пример.
Электрон находится в р-состянии (l=1, m=0,![]() 1). Следовательно, Mz=0, Mz=+
1). Следовательно, Mz=0, Mz=+![]() ;-
;-![]()
Итак.
1. ![]() , описывающая поведение электрона в атоме,
является функцией трех квантовых чисел, так как электрон в атоме имеет три
степени свободы.
, описывающая поведение электрона в атоме,
является функцией трех квантовых чисел, так как электрон в атоме имеет три
степени свободы.
2. В каждом квантовом состоянии, которому соответствуют определенные значения квантовых чисел l, m и n, электрон обладает определенными (дискретными) значениями трех характеристик: En, M, Mz.
3.электрон
обладает собственным механическим моментом, который получил название спина. Msz=ms![]() ;
ms=
;
ms=![]() S; ms- спиновое магнитное квантовое число.
S; ms- спиновое магнитное квантовое число.
S-
спиновое число. Sэл=1/2;
Mzs=![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.