







одинаковые дифференциальные уравнения имеют идентичные решения при идентичных граничных условиях.
Заметим, что уравнение Лапласа описывает также стационарное распределение температуры в однородной среде при отсутствии в ней источников тепла. Поэтому электрическое поле в слабопроводящей среде будет моделировать и распределение температур в теплопроводной среде, если распределение температуры на границах среды будет соответствовать потенциалам электродов. Кроме моделирования температурного поля, электрическое поле способно моделировать гидродинамические потоки в идеальной жидкости.
Принципиальная схема установки изображена на рис. 2.
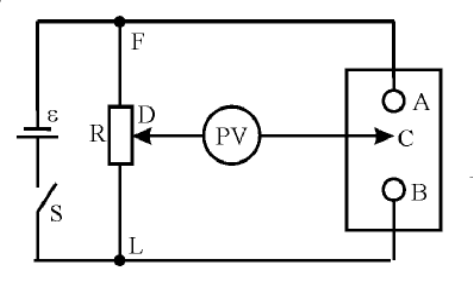
Рис. 2.
При помощи потенциометра R можно произвольно задавать потенциал точки D (приняв за нуль, например, потенциал точки L ). Перемещая зонд C вдоль электропроводной бумаги, можно добиться того, чтобы вольтметр PV показал нуль. При этом потенциал точки C будет равен потенциалу точки D. Множество точек, определенных таким образом, соответствует поверхности постоянного, заданного в точке D потенциала.
При помощи пантографа эти точки переносятся на чертеж в масштабе 1:1. Потенциометр R выполнен в виде отдельных секций, что позволяет регулировать напряжение ступенями. К лабораторной работе прилагается набор листов электропроводной бумаги с различными по форме электродами. Установка позволяет определять вектор напряженности в любой точке поля. Суть метода определения состоит в следующем. Введем систему координат с началом в интересующей нас точке поля (рис. 3).
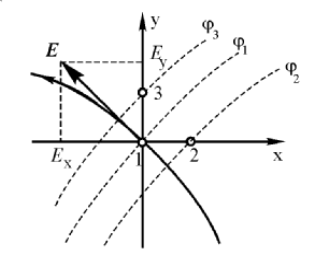
Рис. 3.
Используя формулу (6) для направлений Х и У, получаем:
-
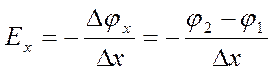 (8)
(8)
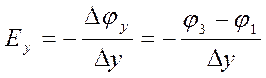 (8')
(8')
На линейке пантографа расположены отверстия, соответствующие точкам 1, 2, 3. Точки 1 и 2 разнесены по координате Х на расстояние ∆x, а точки 1 и 3 - по координате У на расстояние ∆y (∆x = ∆y = 1 см). Поэтому, измерив приращение потенциала ∆φx и ∆φy вдоль осей координат, можно найти проекции Ex , Ey , и построить вектор E. Для маштабного переноса точек на чертеж на линейке справа имеются отверстия 1,2,3 для зонда, а слева - отверстие для переноса точки 1 на чертеж.
1. Установите планшет с моделируемым полем на стенд и подключите электроды к источнику напряжения.
2. Подключите вольтметр к клеммам в соответствии с рис. 2: один конец подключите к точке D, другой будет являться зондом C.
3. В левую часть планшета под зажимы установите лист миллиметровой бумаги формата А4. При помощи пантографа перенесите изображение электродов на чертеж. Укажите полярность электродов.
4.Найдите ряд точек с потенциалом 2 В. Для этого ручку потенциометра R установите в соответствующее положение. Перемещая зонд от одного электрода к другому, добейтесь нулевого показания вольтметра. При помощи пантографа перенесите положение этой точки на чертеж. Переместив зонд немного в сторону, найдите другую точку с тем же потенциалом. Зафиксировав положение 6-8 точек, соедините их плавной линией.
ВНИМАНИЕ: Нулевое показание цифрового вольтметра зафиксировать сложно. С достаточной точностью оно определяется в момент перемены знака напряжения на индикаторе полярности.
5. Аналогично получите эквипотенциальные линии для 3, 4, 5, 6, 7 и 8 вольт.
6. Определите компоненты вектора в точке поля, указанной преподавателем. Для этого поместите в эту точку отверстие 1 линейки, соответствующее началу координат. Отсоединив второй провод вольтметра от потенциометра R, измерьте разности потенциалов ∆φx между точками 1 и 2 и ∆φy между точками 1 и 3. Результаты занесите в отчет (с указанием знака!).
Для правильного определения на индикаторе знака ∆φ общая клемма вольтметра, обозначенная знаком [*], должна быть подключена к началу координат (точка 1), а другая клемма - к точке 2 или 3. В этом случае потенциалы точек 2 и 3 будут указаны по отношению к точке 1, а не наоборот.
По формулам (8) вычислите компоненты Ex , Ey (учтите, что ∆x = ∆y = 1 см.).
7. На чертеже в точке 1 постройте оси координат, отложите проекции Ex и Ey в выбранном масштабе и постройте вектор E
8. Учитывая связь между эквипотенциальными поверхностями и силовыми линиями, постройте на чертеже 5-6 силовых линий. Проверьте, соответствует ли направление построенного вектора E положениям теории.
1. Дайте определение напряженности электростатического поля E и потенциала φ.
2. Что называется силовой линией и эквипотенциальной поверхностью? Почему силовые линии перпендикулярны к эквипотенциальным поверхностям?
3. Какая существует связь между напряженностью и потенциалом? Поясните эту связь графически. Объясните метод определения напряженности поля в данной работе.
4. В чем состоит метод моделирования, используемый в работе
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.