заданию преподавателя строим планы ускорений для второго, четвёртого и одиннадцатого положений механизма
Рассмотрим пример построения плана ускорений для второго положения. Задаёмся масштабным коэффициентом плана ускорений, котрый вычисляется по формуле (10):
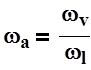 (10)
(10)
wа=0,0025 ![]()
Выбираем произвольно точку p (полюс плана ускорений). Так как точка В движется с постоянной скоростью, то ускорение точки В направлено к центру вращения кривошипа. В выбранном масштабе откладываем длину вектора ab . Получаем точку b .На плане ускорений все точки обозначаем малыми латинскими буквами со штрихом. Звено 3 совершает плоско-параллельное движение. Его ускорение описывается уравнением(11):
aСB=aСBn+aСBt (11)
Направление aСBn известно – направлено вдоль третьего звена в сторону точки вращения, то есть точки В. Значение его вычисляем по следующей формуле(12):
V2CB
aСBn ![]() =
(12)
=
(12)
lCB
Из полюса проводим горизонтальную линию (вдоль которой движется ползун С). Из конца вектора aСBn проводим вектор тангенсального ускорения aСBt , перпендикулярный третьему звену механизма до пересечения с горизонтальной линией. В месте пересечения получаем точку с. Далее рассматриваем 5-ое звено. Оно также совершает плоско-параллельное движение, следовательно его ускорение описывается уравнением(12):
aDC= aDCn +aDCt(12)
Направление aDCn известно – направлено вдоль пятого звена в сторону точки вращения, то есть точки С. Значение его вычисляем по следующей формуле(13):
V2DC
aDCn ![]() = (12)
= (12)
lDC
Из полюса проводим вертикальную линию (вдоль которой движется ползун D). Из конца вектора aDCn проводим вектор тангенсального ускорения aDCt , перпендикулярный пятому звену механизма до пересечения с вертикальной линией. В месте пересечения получаем точку d.
Таким образом построили план ускорения для второго положения механизма. Используя данный алгоритм строим оставшиеся планы ускорений. Во избежание загромождения чертежа каждый план ускорений вычерчиваем отдельно.
1.3. Структурный анализ механизма пресса
Для того, чтобы осуществить переход от кинематического анализа к динамическому с учётом КПД рычажного механизма поступаем следующим образом.
В масштабе вычерчиваем силу полезного сопротивления от перемещения (РПС) точки рычажного механизма, принадлежащей его выходному звену. По горизонтальной оси откладываем перемещение SDi , взятое с плана положения механизма для участка рабочего хода. В этой же системе координат строим график в виде зависимости VD (SDi). Мощность от сил полезного сопротивления при поступательном движении входного звена (13):
NПC(i)=PПC(i)* VD(i) (13)
Перемножаем действительные величины PПC(i) на соответствующие VD(i) , находим NПC(i)
. NПC(i)=YPпс(i) mP (PV mV) [Вт]
Для каждого положения находим:
![]()
![]()
![]()
![]()
![]()
![]()
По найденным таким образом значениям мощности строим график NПC (SDi).
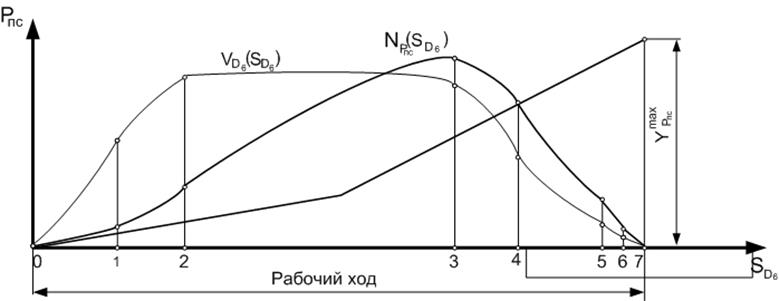
По построенному графику определяем и находим наиболее нагруженное положение механизма, соответствующее пику (max) мощности. Для расчёта крутящего момента на входном валу редуктора необходимо учесть потери на трение в кинематических парах 6-ти звенного рычажного механизма. Будем считать ля всех с учётом наличия в нём кроме вращательных и поступательных пар h=0,7.
NPпс= РПС VD=Т2 w2 (14)
NPпсmax
![]() Т2= (15)
Т2= (15)
w2
2237,25
![]() Т2= =237,5
Т2= =237,5
9,42
Т2
![]() Т2потр= (16)
Т2потр= (16)
h
237,5
![]() Т2потр=
=339,3
Т2потр=
=339,3
h
1.4. Приведение сил производственных сопротивлений к валу кривошипа
Механизм машинного агрегата - многозвенная система, нагруженная силами и моментами, приложенными к различным её звеньям. При построении модели механизма, все силы и моменты, приложенные к нему, оказываются приведенными к одному звену - звену кривошипа и замененные
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.