


механизмов, помещенный в отдельный корпус и предназначенный для изменения параметров мощности.
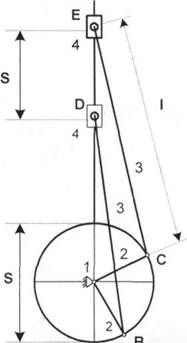
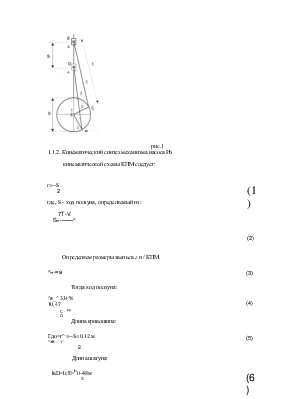
рис.1
1.1.2. Кинематический синтез механизма насоса Из кинематической схемы КПМ следует:
|
(1) (2) |
r=--S
2
где, S - ход ползуна, определяемый из:
7T-V S=-——^
Определяем размеры звеньев г и / КПМ.
|
(3) (4) |
^=-=а
Тогда ход ползуна:
^я_^ 3J4^8
10,47
|
СО |
кр
|
(5) |
Длина кривошипа:
Гдо=г^ =--S=0,12 м
"АВ ~' ^С
2
|
(6) |
Длина шатуна:
lвD=lcE=l=0-48м
Л
10
1.2. Кинематический анализ.
1.2.1. Определение функций положений и построение планов механизмов
Для построения планов механизма выбираем масштабный коэффициент
/^/ и вычисляем отрезки чертежа.
АВ=АС=1^ (7)
^
BD=CE=1^ (8) ^i
Радиусом равным АВ проводим окружность, а т.к. кривошипы АВ и АС имеют равномерное вращательное движение и совершают полный оборот, то делим окружность на 12 равных частей, через каждые 30°. Каждое положение точек В и С обозначаем определенным номером.
Для определения крайних положений КПМ из точки А делаем засечки, радиусами (1+г) и (г"1) по прямой A-D-E (по вертикали), по которой движется ползун, и находим ход ползуна, который равен S = 2 • г. Построение плана механизма начинаем для заданного положения (2, 4, 6, 7, 8 положение). Устанавливаем точку В в заданное положение, далее из точки 5ц радиусом равным BD делаем засечку на линии движения точки D (т.е. по вертикали), полученную точку BD соединим прямой линией с точкой В^ и определим положение шатуна BD в позиции 11. При точке D^ изображаем поршень, который движется в неподвижных направляющих.
Аналогично строим планы механизма для остальных 11 положений. Далее задаемся положением второго кривошипа АС, который смещен относительно другого на 90°. Точка С будет находиться в 8 положении. Аналогично из точки С радиусом СЕ делаем засечку на линию движения точки Е по направляющей поршня. Полученную точку Е соединяем прямой линией с точкой С, и определяем тем самым положение шатуна СЕ в 8 положении. При точке Eg изображаем поршень (прямоугольник). Аналогично и для других положений.
•^
1.3. План скоростей
1.3.1. Построение планов скоростей
Величина скорости точки В определяется по формуле:
vb-iab-^kp- 0,12-10,47= 1,2564м/с (9)
а направление в соответствии с направлением со кривошипа (JL АВ).
Модуль скорости точки В (Ув) равен модулю скорости точки С и постоянен для всех положений.
Связь между скоростью точки D и скоростью точки В (обе точки принадлежат звену 3) задаемся векторным уравнением
vd-vi^+vdb (10)
где,Ув10В,Уо1АВЕ
Здесь и в дальнейшем вектор известный по величине и направлению подчеркиваем двумя линиями, а вектор известный только по направлению -одной линией.
Для определения указанных неизвестных скоростей (элементов) строим план скоростей. Выбрав масштабный коэффициент, Цу вычисляем отрезок
РЬ = — ^ изображающий скорость Vg. В соответствии с уравнением ^v
откладываем от произвольной точки Р (полюс плана скоростей) найденный отрезок РЬ, и через конец этого отрезка (точка Ь) проводим линию перпендикулярную BD. Через точку Р проводим линию параллельную АЕ. В пересечении указанных линий ставим точку d, теперь отрезок Pd изображает скорость vd в точке d, а отрезок bd скорость vdb • Находим значение действительных скоростей
V^^v-Pd (11) V^-Hv-bd (12)
-fi
а также находим угловую скорость соз:
»з = уто (13)
^db
Находим значение модуля Vp, для всех 12 положений, а т.к. кривошипы смещены относительно друг друга до 90°, то можно найти и значение модуля V^ по следующим зависимостям:
^i = ^90°) (14)
1.4.План ускорений 1.4.1. Построение планов ускорений
Ускорение точек В (С), совершающей движение по окружности радиуса г равны:
а^а^+а^=13,15(м/с2) (15)
гдe,aвn=r.co^)2=OД2•10Л72-13J5 (м/с2); а^ ^r-s^) ^O; т.к.
5со „ £ = — = 0, т.к. со^ = const д1
Модули ускорений точек В и С равны (а^ = а^) и постоянны для всех 12
положений. Векторы ag и а^ направлены вдоль прямых АВ и АС к центру А, для каждого положения.
Выбрав масштабный коэффициент |Ыд для изображения ускорений вычисляем длину отрезка изображающего ag. Затем из произвольной точки П
(полюс плана ускорений) откладываем а^ = а^ , в виде отрезка ПЬ и находим полное ускорение точки В (С).
Для определения ускорений любой точки Di=Ei запишем уравнение:
а? = ар + а^рв + а^в (16)
n V DB
здесь a db = ——— ^ и направлено оно от точки D к точке В (a'oa -L DB ). Мы
^DB
знаем, что а^ параллельно направляющей ползуна (по вертикали).
Отложив от точки. В отрезок bd соответствующий zl^db проводим через
," точку d линию перпендикулярную dB.Через полюс тг проводим линию параллельную направляющей ползуна (по вертикали). Эти линии пересекаются в точке d . Отрезок nd - представляет собой искомое ускорение точки
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.