Методы приближенного вычисления корней нелинейных уравнений (Практическая работа № 5)

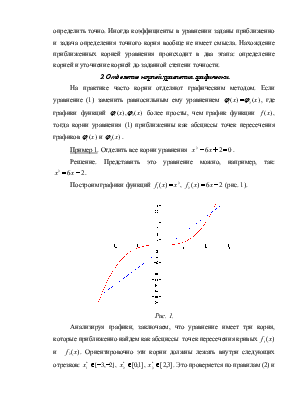
которые приближенно найдем как абсциссы  точек пересечения кривых  и  . Ориентировочно эти корни должны лежать внутри следующих отрезков: , , . Это проверяется по правилам (2) и (3). Для корня  получаем: , , т.е. условие (2) выполняется; поскольку ; получаем также , , т.е. условие (3) выполняется.

Следовательно, на отрезке  отделен один корень.

Аналогичная проверка проводится и для корней  и .  

3. Отделение корней аналитически

Прежде чем отделять   корни уравнения, естественно найти границы области, в которой расположены   все корни уравнения, поэтому мы сначала приведем ряд способов отыскания этих границ.

Для алгебраического уравнения

                                   (2)

задача отделения корней решается более просто и точно. Прежде чем отделять   корни уравнения, естественно найти границы области, в которой расположены   все корни уравнения, поэтому мы сначала приведем ряд способов отыскания этих границ.

Пусть

Теорема 1.  Все корни уравнения (1) расположены   в кольце

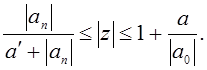                                                                                       (3 )

Предположим, что все коэффициенты уравнений – действительные числа и

> 0. Найдем границы действительных корней уравнения. Очевидно, достаточно иметь  способы  определения  границ  положительных корней, так как, заменяя х на

– x, мы получим уравнение, корни которого отличаются от корней исходного уравнения знаком.

Теорема 2. Обозначим через а максимум абсолютных величин отрицательных коэффициентов уравнения, и пусть первый отрицательный коэффициент в ряду  есть . Тогда все положительные корни уравнения  меньше 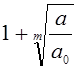 . (Если отрицательных  коэффициентов нет, то нет и положительных корней).

С помощью теоремы 2 можно найти границы действительных корней очень грубо. Иногда эти границы можно сузить, применив следующий простой прием.

Пусть в уравнении коэффициенты  неотрицательны, а  неположительны и < 0. Введем обозначения:

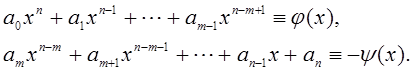
Тогда

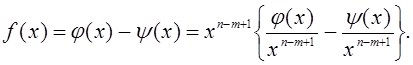
Первое слагаемое в скобках содержит только положительные степени , а второе  – только отрицательные. Следовательно, при  первое слагаемое возрастает, а второе убывает с возрастанием , т. е. при  функция f(x) возрастает вместе с х. Найдя какое-либо , для которого , мы можем гарантировать, что все корни уравнения меньше .

В общем случае представим f(x) в  виде

где F(x) есть многочлен, содержащий все первые старшие по степени члены многочлена f(x), имеющие положительные коэффициенты и все члены с отрицательными коэффициентами, а Ф(х) — многочлен, образованный всеми остальными членами исходного многочлена f(x). Тогда, если мы найдем , для которого  то  при всех , так как  при  и все корни уравнения  будут меньше .

Хороший способ отыскания верхней границы положительных корней указал Ньютон. Этот способ основан на утверждении: если при  имеют место неравенства

                                                           (4)

то уравнение f(x) = 0 не имеет корней, больших .

Таким образом, способ Ньютона заключается в отыскании значения а>0, при котором многочлен f(x) и все его производные имеют положительное значение. Тогда это значение будет верхней границей положительных корней.

Замечание. Нижняя граница положительных корней может быть найдена из уравнения  такими же приемами, так как если есть верхняя граница положительных корней этого уравнения, то  будет нижней   границей    положительных корней исходного уравнения.

Пример 2.  Найти границы действительных корней уравнения

.

Решение. 1- й способ (использование теоремы 1). В данном случае

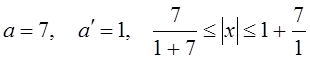
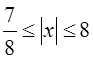
Следовательно, все корни уравнения находятся на отрезке .

2-й способ (использование теоремы 2). В данном случае

Следовательно, все положительные корни уравнения меньше

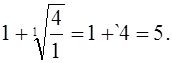
Для отыскания нижней границы положительных корней уравнения заменим х на  и  рассмотрим уравнение    .

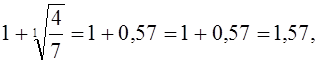Так как  то верхняя граница положительных корней этого уравнения будет:  а следовательно, нижняя граница корней исходного уравнения .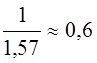

Итак, все положительные корни уравнения находятся на отрезке . Для отыскания границ отрицательных корней рассмотрим уравнение

получающееся заменой х на . В данном случае получаем

Следовательно, все положительные корни уравнения меньше

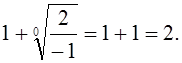
Для отыскания нижней границы положительных корней уравнения заменим  на  и  рассмотрим уравнение    .

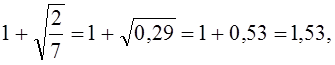Так как  то верхняя граница положительных корней этого уравнения будет:  а следовательно, нижняя граница корней исходного уравнения 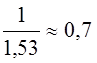. Получаем,  все положительные корни уравнения находятся на отрезке , т. к. , то все отрицательные корни уравнения находятся на отрезке . Следовательно, все корни уравнения находятся на отрезке . Получен значительно лучший результат, чем в первом способе.

3-й способ. Представим

в виде

где

При

Поэтому все корни уравнения меньше 20.

Для отыскания нижней границы снова заменим  х на  и  рассмотрим уравнение    . Получим:

где

. Таким образом, положительные корни уравнения меньше 1, а положительные корни исходного уравнения больше . Следовательно, корни уравнения  расположены на отрезке . Границы  отрицательных  корней  можно  получить, если ввести замену  (см. 2-й способ).

4. Число действительных корней алгебраического уравнения

Точное число корней алгебраического уравнения, заключенных в данных пределах, может быть определено с помощью теоремы Штурма.

Теорема Штурма. Пусть дано алгебраическое уравнение степени n, не имеющее кратных корней; найдем производную  и обозначим остаток от деления f(x) на  взятый с обратным знаком, через ; остаток от деления на с обратным