














ПРАКТИЧЕСКАЯ РАБОТА № 8
ИНТЕРПОЛИРОВАНИЕ И ЭКСТРАПОЛИРОВАНИЕ ФУНКЦИЙ
Цель – освоение основных приемов применения интерполяционных формул Ньютона и схемы Эйткена; возможность применять данные формулы для нахождения аргумента функции по заданной таблице значений функции.
ОБЩИЕ СВЕДЕНИЯ
1) Интерполяционные формулы Ньютона а) Первая интерполяционная формула Ньютона имеет вид:
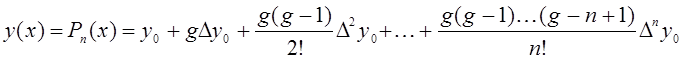 , (1) где
, (1) где
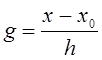 ,
, ![]() ,
, ![]() ,
,
Число n желательно
выбирать так, чтобы разности ![]() были практически постоянными.
были практически постоянными.
Остаточный член ![]() формулы
имеет вид:
формулы
имеет вид:
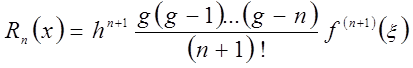 ,
(2) где
,
(2) где ![]() – некоторая внутренняя
точка наименьшего промежутка, содержащего все узлы
– некоторая внутренняя
точка наименьшего промежутка, содержащего все узлы ![]()
![]() и точку
и точку ![]() .
.
При наличии дополнительного
узла ![]() на практике пользуются более удобной
приближенной формулой.
на практике пользуются более удобной
приближенной формулой.
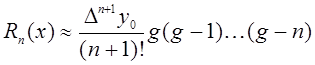 .
(3)
.
(3)
Первая формула Ньютона применяется для интерполирования и экстраполирования
в точках ![]() , близких к началу таблицы
, близких к началу таблицы ![]() .
.
![]() – конечная разность n-го порядка, причем:
– конечная разность n-го порядка, причем:
если n=1, то получается формула линейной интерполяции
![]() ;
(4)
;
(4)
если n=2, то получается формула квадратичной интерполяции
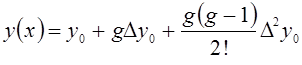 .
(5)
.
(5)
Пример 1. По данной таблице значений функции y = lgxнайти lg 1001.
Решение. Составляем таблицу разностей, записывая их в единицах седьмого разряда, и замечаем, что третьи разности практически постоянны.
|
х |
y |
Dy |
D2y |
D3y |
|
1000 |
3,0000000 |
0,0043214 |
- 0,0000426 |
- 0,0000008 |
|
1010 |
3,0043214 |
0,0042788 |
- 0,0000418 |
- 0,0000009 |
|
1020 |
3,0086002 |
0,0042370 |
- 0,0000409 |
- 0,0000008 |
|
1030 |
3,0128372 |
0,0041961 |
- 0,0000401 |
|
|
1040 |
3,0170333 |
0,0041560 |
||
|
1050 |
3,0211893 |
Поэтому в формуле (1) достаточно взять n=3:
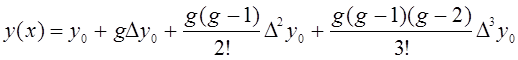 .
.
Для х=1001 имеем g=0,1. Таким образом:
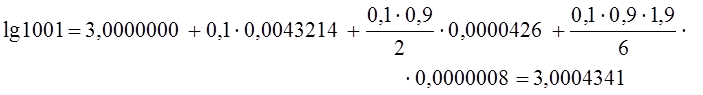
Оценим остаточный член. По формуле (2) при n=3 имеем
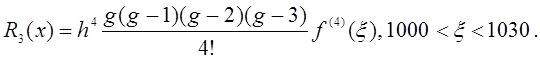
Так как f(x)=lgx, то 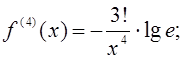 поэтому
поэтому 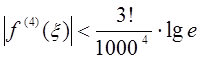 .
.
При h=10 и g=0,1 окончательно получаем
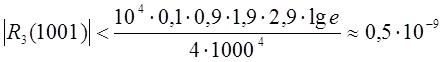 .
.
Таким образом, остаточный член может повлиять только на девятый десятичный знак. Заметим, что полученное значение lg 1001 полностью совпадает со значением в семизначной таблице логарифмов.
б) Вторая интерполяционная формула Ньютона имеет вид:
![]()
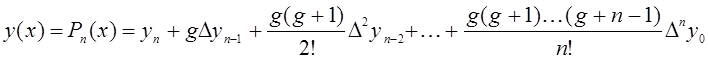 (6)
(6)
где 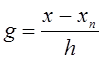
Остаточный член ![]() формулы имеет вид
формулы имеет вид
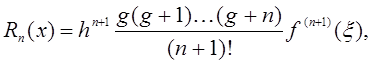 (7)
(7)
где ![]() - внутренняя точка наименьшего промежутка,
содержащего все узлы
- внутренняя точка наименьшего промежутка,
содержащего все узлы ![]() и точку
и точку ![]() .
.
Вторая формула Ньютона используется для интерполирования и экстраполирования
в точках ![]() , близких к концу таблице, т.е. к
, близких к концу таблице, т.е. к ![]() .
.
Пример 2. Используя таблицу значений функции y=sinx, найти sin 54° и
sin 56° и указать погрешность результатов.
Решение. Составив таблицу разностей, видим, что третьи разности практически постоянны. Поэтому в формуле (6) достаточно взять четыре члена.
Для вычисления sin 54° имеем
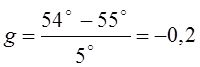 .
.
По формуле (6) получаем
![]()
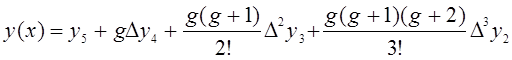
|
х |
y |
Dy |
D2y |
D3y |
|
30° |
0,5000 |
0,0736 |
- 0,0044 |
- 0,0005 |
|
35° |
0,5736 |
0,0692 |
- 0,0049 |
- 0,0005 |
|
40° |
0,6428 |
0,0643 |
- 0,0054 |
- 0,0003 |
|
45° |
0,7071 |
0,0589 |
- 0,0057 |
|
|
50° |
0,7660 |
0,0532 |
|
|
|
55° |
0,8192 |
|
|
|
![]()
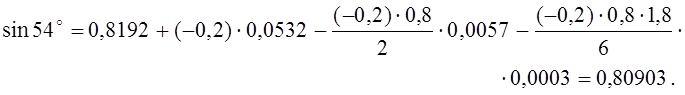
Остаточный член при n=3 имеет вид
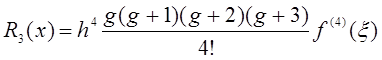 .
.
В нашем случае h=5° =0,0873, g= - 0,2, f(4) (x) = sinx£ 1. Таким образом:
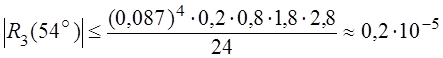 .
.
Отсюда видно, что остаточный член может повлиять только на пятый десятичный знак; поэтому окончательный результат записываем в виде
sin 54° =0,8090 .
Полученное значение полностью совпадает с табличным.
Найдем
теперь sin 56°.
В этом случае 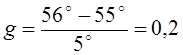 ,
и по формуле (6) получаем
,
и по формуле (6) получаем
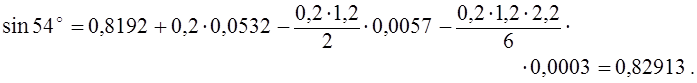
Остаточный член при h=0,0873, g= 0,2 оценивается следующим образом:
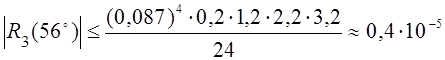 .
.
Таким образом, остаточный член может повлиять лишь на пятый знак. Поэтому принимаем
sin 56°=0,8291.
2) Интерполяционная формула Лагранжа:
Пусть ![]()
![]() – произвольные узлы, а
– произвольные узлы, а
![]() – значения функции
– значения функции ![]() . Многочленом степени
. Многочленом степени ![]() , принимающем в точках
, принимающем в точках ![]() значения
значения ![]() , является
интерполяционный многочлен Лагранжа
, является
интерполяционный многочлен Лагранжа
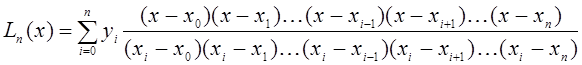 . (8)
. (8)
Остаточный член равен
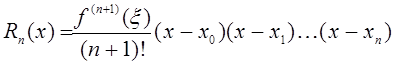 , (9)
, (9)
где ![]() – некоторая точка
наименьшего промежутка, содержащего все узлы
– некоторая точка
наименьшего промежутка, содержащего все узлы ![]()
![]() и точку
и точку ![]() .
.
Если требуется найти не общее выражение ![]() , а лишь
его значения при конкретных
, а лишь
его значения при конкретных ![]() и при этом значения
функции даны в достаточно большом количестве узлов, то удобно пользоваться
интерполяционной схемой Эйткина. Согласно этой схеме последовательно
вычисляются многочлены
и при этом значения
функции даны в достаточно большом количестве узлов, то удобно пользоваться
интерполяционной схемой Эйткина. Согласно этой схеме последовательно
вычисляются многочлены
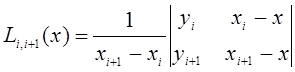
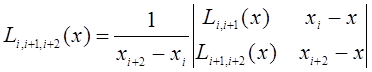
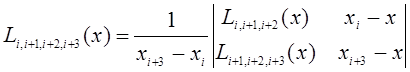 и т.д.
и т.д.
Интерполяционный многочлен ![]() - й
степени, принимающий в точке
- й
степени, принимающий в точке ![]() значения
значения ![]()
![]() , запишется следующим
образом
, запишется следующим
образом
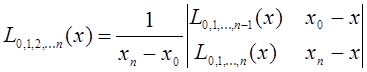
Вычисления по схеме Эйткина удобно расположить в таблице.
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
||
|
4 |
|
|
|
Вычисления по схеме Эйткина обычно ведут до тех пор, пока последовательные
значения ![]() и
и ![]() не совпадут в пределах заданной
точности.
не совпадут в пределах заданной
точности.
Пример 3. Функция задана таблицей.
|
x |
1,0 |
1,1 |
1,3 |
1,5 |
1,6 |
|
y |
1,000 |
1,032 |
1,091 |
1,145 |
1,170 |
Применив
схему Эйткена, найти ![]() .
.
Решение. Записываем данные значения функции в таблицу и вычисляем разности x-xi при x=1,15.
|
i |
xi |
yi |
xi-x |
Li,i+1 |
Li,i+1,i+2 |
|
0 |
1,0 |
1,000 |
- 0,15 |
1,048 |
1,048 |
|
1 |
1,1 |
1,032 |
- 0,05 |
1,047 |
|
|
2 |
1,3 |
1,091 |
0,15 |
1,050 |
|
|
3 |
1,5 |
1,145 |
0,35 |
1,057 |
|
|
4 |
1,6 |
1,170 |
0,45 |
Затем последовательно находим многочлены первого порядка:
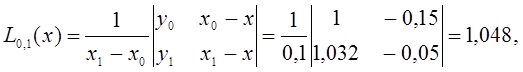
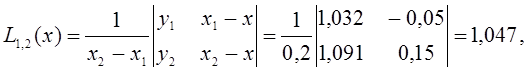
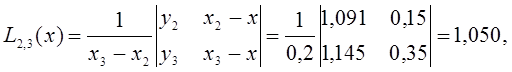
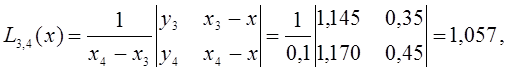
Полученные значения ![]() заносим
в таблицу, после чего вычисляем
заносим
в таблицу, после чего вычисляем
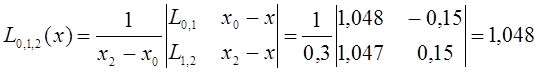
Значения
![]() и
и ![]() совпадают до третьего знака. На этом вычисления можно
прекратить и с точностью до 10-3 записать:
совпадают до третьего знака. На этом вычисления можно
прекратить и с точностью до 10-3 записать:
![]()
Вопросы для самоконтроля
1. В какой форме ставится задача интерполирования?
2. В какой постановке задача интерполирования называется параболической?
3. Какие точки называются узлами интерполяции?
4. Какие узлы интерполяции называются равноотстоящими?
5. Когда используются интерполяционные формулы?
6. Что должно учитываться при оценке погрешности результатов?
7. Что означает «интерполирование в узком смысле слова»?
8. Что подразумевается при решении задачи экстраполирования?
9. При решении каких задач используется первая интерполяционная
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.