Специальная теория относительности (СТО или релятивистская механика)

ЭЛЕМЕНТЫ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ

В основе специальной теории относительности (СТО или релятивистской механики) лежат два постулата.

Первый постулат. Любое физическое явление в различных инерциальных системах отсчета при одних и тех же условиях протекает одинаково. Этот постулат часто называют принципом относительности Эйнштейна, т. к. он является обобщением механического принципа относительности Галилея на все явления природы. Первый постулат СТО соответствует тому, что любой закон природы (физики) во всех инерциальных системах отсчета имеет один и тот же вид.

Второй постулат. Скорость света в вакууме (с) одинакова для всех инерциальных систем отсчета. Она не зависит ни от скорости источника, ни от скорости приемника светового сигнала. Этот постулат противоречит закону сложения скоростей классической механики. Это существенно только для достаточно больших скоростей тел (близких к скорости света). А классическая механика, как оказалось, справедлива только для достаточно малых скоростей тел. В этом случае закон сложения скоростей оказывается справедливым с очень большой точностью.

Из постулатов СТО вытекают некоторые, исключительно важные для практики, следствия.

Предельность скорости передачи сигнала. Скорость света в вакууме является предельной скоростью, с которой может передаваться сигнал (информация, взаимодействие между телами). Любое тело в любой инерциальной системе отсчета может двигаться только со скоростью, меньшей скорости света.

Относительность одновременности двух событий. Два события, происходящие в различных точках одной инерциальной системы отсчета одновременно (по часам этой системы), в другой инерциальной системе отсчета не будут одновременными (по ее часам). Относительность одновременности соответствует различному течению времени в различных инерциальных системах отсчета.

Относительность расстояний. Длина тела максимальна в системе отсчета, относительно которой это тело покоится (система  К  с осями  0X, 0Y, 0Z  на рисунке 38). Эта длина называется собственной длиной тела  (l₀). Длина тела (l) в системе отсчета, относительно которой тело движется (система  К₁  с осями  0₁X₁, 0₁Y₁, 0₁Z₁) со скоростью  , уменьшается в соответствии с формулой

.

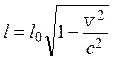Здесь под длиной понимается размер тела в направлении, параллельном скорости    (продольный размер). Поперечные размеры тела одинаковы в любых инерциальных системах отсчета. Длина тела в системе отсчета, относительно которой оно движется, определяется как разность координат (положений) его концов, измеренных одновременно по часам этой системы. Приведенная формула выражает так называемое релятивистское сокращение размеров тела в движущихся системах отсчета.

Относительность промежутков времени. Промежуток времени между двумя событиями минимален в той системе отсчета (К₁), в которой события происходят в одной и той же точке. Этот промежуток времени называется собственное время (t₀). Промежуток времени (t) между этими же событиями в системе отсчета  К (отсчитанный по часам этой системы), движущейся относительно системы  К₁  со скоростью  , всегда больше собственного времени и связан с ним соотношением

.

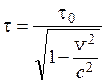Собственное время отсчитывается по часам, движущимся вместе с системой отсчета. Часы, движущиеся относительно инерциальной системы отсчета, идут медленнее неподвижных часов и показывают меньший промежуток времени между событиями. Приведенная формула выражает так называемое релятивистское замедление времени.

Релятивистский закон сложения скоростей. Если тело (материальная точка)  А  движется относительно инерциальной системы отсчета  К  со скоростью  , а сама система отсчета  К  движется относительно другой инерциальной системы отсчета  К₁  со скоростью  , то скорость тела относительно системы отсчета    не равна векторной сумме скоростей    и    (как это было в классической механике). Для простого случая, когда скорости    и    параллельны между собой и направлены в одну сторону (рисунок 39), релятивистский закон сложения скоростей выражается формулой

.

Эту же формулу можно использовать и в случае противоположного направления скоростей    и  ; при этом вместо модулей всех скоростей в формуле будут фигурировать их проекции (соответственно на оси  0X  и  0₁X₁).

Из приведенной формулы следует, что сумма двух скоростей, меньших или равных  с, есть скорость, также меньшая или равная  с. В частности, если  v = c, то и  v₁ = c  при любой скорости  u. Это соответствует второму постулату (движение света в различных системах отсчета).

Из приведенных соотношений, математически выражающих следствия постулатов СТО, вытекает, что в случае малых скоростей (v << c) все закономерности, присущие релятивистской кинематике, переходят в закономерности классической механики. Например, релятивистский закон сложения скоростей переходит в закон сложения скоростей классической механики:  v₁ = v + u. Таким образом, классическая механика является предельным случаем СТО (для малых по сравнению со скоростью света скоростей).

В СТО масса тела зависит от системы отсчета. В инерциальной системе отсчета, относительно которой тело покоится (система движется вместе с телом), его масса принимает минимальное значение. В этом случае она называется масса покоя (m₀). В системе отсчета, относительно которой тело движется со скоростью  , его масса (релятивистская масса) возрастает и определяется с помощью соотношения

.

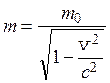Соотношение, определяющее импульс тела, остается таким же, как и в классической механике, только под массой в нем понимается именно релятивистская масса тела

.

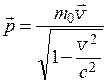В силу этой формулы импульс тела не пропорционален его скорости.

Второй закон Ньютона в форме    оказывается несправедливым. Однако выраженный через импульс тела, закон сохраняет такую же форму, как и в классической механике

.

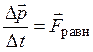Следует помнить, что импульс тела здесь определяется вышеприведенной формулой.

Важнейшим следствием специальной теории относительности является универсальная связь между полной энергией любого тела (Е) и его массой

.

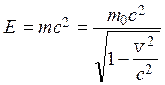При изменении энергии системы тел соответственно изменяется и ее масса

.

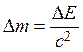В обыденных условиях (нагревание тел, химические реакции и т. п.) изменения энергии настолько малы, что обнаружить соответствующие изменения массы невозможно. Однако для внутриядерных процессов изменение энергии оказывается достаточно большим, чтобы обнаруживалось изменение массы.

Согласно формуле взаимосвязи энергии и массы тело обладает определенной энергией и находясь в покое (относительно какой-нибудь инерциальной системы отсчета). Эта энергия называется энергией покоя (Е₀):

.

Наблюдаются процессы, при которых элементарные частицы, обладающие ненулевыми массами покоя, при взаимодействии превращаются в частицы, масса покоя каждой из которых равна нулю. При этом энергия покоя исходных частиц полностью превращается в кинетическую энергию образовавшихся частиц.