ЛАБОРАТОРНАЯ РАБОТА №17
ОПРЕДЕЛЕНИЕ ПОСТОЯННЫХ ПЛАНКА И РИДБЕРГА
С ПОМОЩЬЮ МОНОХРОМАТОРА УМ-2
Цель работы: определить постоянные Планка и Ридберга экспериментальным путем.
Приборы и принадлежности:монохроматор УМ-2, ртутная лампа с источником питания, трубка с узлом крепления, высоковольтный индуктор, источник питания на 12В, кювета, раствор двуххромовокислого калия, подъемный столик.
Нагретое до определенной температуры тело становится источником излучения электромагнитных волн различной длины, в том числе и оптического диапазона. В спектрах твердых тел и жидкостей существуют волны практически всех длин. Эти спектры называют сплошными. Спектры паров и газов представляют собой набор широких окрашенных полос, разделенных темными промежутками, или отдельные линии, разделенные темными промежутками. Такие спектры обусловлены испусканием электромагнитных волн и объединены общим названием эмиссионных или атомных спектров.
Если на окрашенный раствор направить излучение от источника сплошного спектра, то на его фоне образуются отдельные темные линии. Такой спектр, связан с поглощением веществом отдельных электромагнитных волн, называют абсорбционным спектром или спектром поглощения.
Спектр поглощения используется для определения постоянной Планка. Направим на кювету с раствором двухромовокислого калия (K2Cr2O7) световой поток. Прохождение света через раствор сопровождается его поглощением. Поглощение света приводит к распаду молекулы двухромового кислого калия на ионы. Распад происходит по схеме:
K2Cr2O7 → K2++ + Cr2O7¯ ¯ ( 17.1 )
Экспериментально найдено, что распад происходит, если молекуле Cr2O7 сообщается энергия не ниже, чем 3,97×10-19Дж. Следовательно, минимальная энергия фотонов, поглощенных раствором, равна hv = 3,97×10-19Дж. Отсюда
(
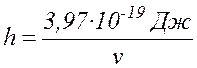17.2 )
где v – минимальная частота.
Учитывая связь частоты с диной
волны (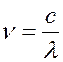
) и подставляя v в формулу (17.2), получим:
(
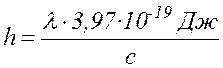17.3 )
где c – скорость света (с = 299792458 м/с » 3×108 м/с),
l – небольшая длина волны в спектре поглощения раствора K2Cr2O7 , определяемая с помощью монохроматора.
Наиболее простым атомным спектром является спектр легчайшего химического элемента - водорода.
В 1885 году швейцарский физик Бальмер, изучая видимую часть этого спектра, экспериментальным путем установил наличие определенной закономерности, связывающей между собой длины волн отдельных спектральных линий. Им установлена формула:
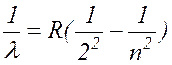( 17.4
)
где n= 3, 4, 5, ... ,
R= 1,097×10-7 м-1 - постоянная Ридберга.
Величину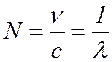 
(
17.5 )
называют волновым числом. Оно показывает, сколько длин волн укладывается в 1м.
Линии в спектре водорода, описываемые формулой (17.4) составляют спектральную серию Бальмера. В видимой области спектра лежат только четыре линии этой серии. В настоящее время обнаружено 29 линий серии Бальмера, 25 из которых лежат в близкой ультрафиолетовой части спектра.
В 1906 году Лайман открыл в далекой ультрафиолетовой области спектра водорода серию линий, описываемых формулой
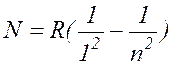, где
n= 2, 3, 4, ... ( 17.6 )
В 1908 году серию линий в близкой инфракрасной области водородного спектра обнаружил Пашен. Она укладывается в формулу
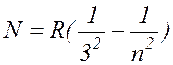, где n= 4,
5, 6, ... ( 17.7 )
И, наконец, Бреккет (1922г.) и Пфундт (1930г.) нашли еще две серии линий в более далеких областях инфракрасной части спектра водорода. Формулы, описывающие эти серии, имеют вид:
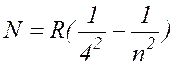, где n= 5, 6, 7, ... ( 17.8 )
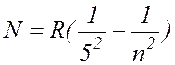, где n= 6, 7, 8, ... ( 17.9 )
Если объединить (17.4), (17.6)-(17.9), то получим объединенную формулу:
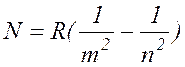( 17.10 )
где число m принимает целые значения m= 1, 2, 3, ... и определяет серию, число n удовлетворяет неравенству n > m и определяет отдельные линии серии. Эти серии приведены на рис. 17.1.
Подставив соотношение (17.5) в (17.10), получим:
(
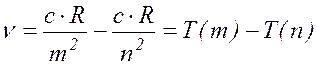17.11 )
Отсюда следует вывод, что частоты
всех линий в спектре водорода могут быть представлены в виде разности двух
функций от целых чисел 
и 
. Эти
функции носят название термов спектральных.
Теория спектра водорода базируется на трех постулатах Бора:
1.
Электрон в
атоме водорода может находиться лишь на орбитах строго определенного радиуса,
называемых стационарными. На этих орбитах момент количества движения электрона mvкrк кратен целому числу 
, т.е.
(
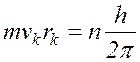17.12 )
где m – масса электрона (m = 9,1 × 10-31кг),
vk – скорость электрона на k-той орбите,
rk – радиус k-той орбиты,
h – постоянная Планка (h = 6,62 × 10-34Дж/с)
n – квантовое число (n = 1, 2, 3, ...)
Рис. 17.1. Схематическое изображение спектральных линий водорода
2. Движение электрона по стационарным орбитам не сопровождается излучением или поглощением энергии.
3. При переходе электрона с одной стационарной орбиты на другую излучается или поглощается квант энергии, частота которого определяется частотным условием Бора:
(
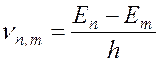17.13 )
где Еn и Еm – соответственно, энергия электрона на n –ой и m –ой орбитах.
Согласно теории, полная энергия электрона в атоме отрицательна и равна
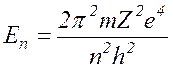( 17.14
)
где m и е – масса и заряд электрона е -= 1,6 × 10-19Кл.
Z – порядковый номер элемента в таблице Менделеева
n – номер орбиты, на которой находится электрон.
Введем обозначения
(
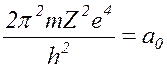17.15 )
Тогда (17.14) перепишется в виде:
(
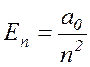17.16 )
Подставив (17.16) в (17.13), получим:
(
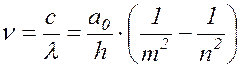17.17 )
Отсюда:
(
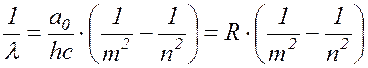17.18 )
т.е. получили формулу, совпадающую с выражением (17.10)
Величину
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
