Уравнения колебаний многомерной системы в формализме Лагранжа в линейном приближении. Определение собственных частот многомерных колебаний в линейном приближении

31.УРАВНЕНИЯ КОЛЕБАНИЙ МНОГОМЕРНОЙ СИСТЕМЫ В ФОРМАЛИЗМЕ ЛАГРАНЖА В ЛИНЕЙНОМ ПРИБЛИЖЕНИИ.

Запишем уравнение в виде Лагранжа-Эйлера:

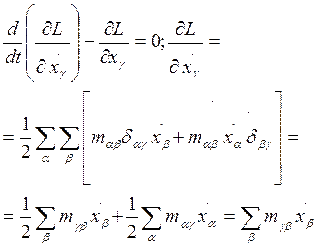
В дальнейшем будем  рассматривать мех.сист. у которых матрицы m и æ являются симметричными.

;

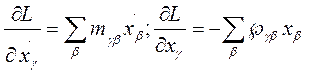
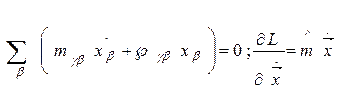
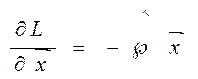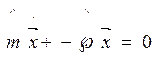
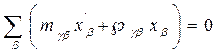
32 ОПРЕДЕЛЕНИЕ СОБСТВЕННЫХ ЧАСТОТ МНОГОМЕРН.КОЛЕБ В ЛИН.ПРИБЛЕЖЕНИИ.

Будем рассматривать р-е ур-ий дв-я кол-ся мех-ой сис-мы в лин прибл.,т.е когда будем строить ф-ю Лагранжа, то   ф-ии будет реализовывать разложение слагаемых до 2ого порядка по оклон. обобщающих координ. от состояния устойчивого равновесия

            L(ϕ,ψ,ϕ,ψ)Пусть механич. сис-ма имеет r степеней свободы. Эта механич. cис-ма определ-ся  обобщ .коорд. коорд-ми q_1,q_2….q_r..Обозначим q_r,где L=1,2….r,тогда L=L(q_λ,q_λ)=T-U(q_λ)

Будем рассматривать  состо-я мех сис-мы,где потенц. энергия минимальна.X_λ=q_λ-q⁽⁰⁾_λ отклон. обобщ. коорд-ты от положения равновесия.U(q_λ)=U(q⁽⁰⁾_λ+x_λ)= U(q⁽⁰⁾_λ)++  +….

T= Ф-ю Лагранжа для колеб. многомерной сис-мы   в лин.приближении можем записать в виде L=  где  координаты опред.пар-ми  коэ-ты

33 РЕШЕНИЕ УРАВНЕНИЙ МНОГОМЕРНЫХ КОЛЕБАНИЙ В ЛИНЕЙНОМ ПРИБЛИЖЕНИИ.

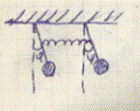
34 ПОСТРОИТЬ ФУНКЦИЮ ЛАГРАНЖА КОЛЕБАНИЯ ДВОЙНОГО МАТЕМАТИЧЕСКОГО МАЯТНИКА В ЛИНЕЙНОМ ПРИБЛИЖЕНИИ.