Интересные задачи для проведения внеклассных мероприятий по математике (Три рыбака и одна лодка. Большая семья. Возраст старика Хоттабыча. Завещание)

Интересные задачи.

1.  Три рыбака и одна лодка. Три рыбака имеют общую лодку, но у каждого из них есть свой замок и ключ к нему. Как прицепить лодку к столбику на берегу, чтобы любой из рыбаков мог отцепить её с помощью только своего ключа?

2.  Большая семья. За обеденным столом собрались: 1 дедушка, 1 бабушка, 2 отца, 2 матери, 4 детей, 3 внука, 1 брат, 2 сестры, 2 сына, 1 свекор, 1 свекровь и 1 невестка. На сколько персон минимально должен быть накрыт стол?

3.  Возраст старика Хоттабыча записывается числом, состоящим из различных цифр. Если первую и последнюю цифру этого числа зачеркнуть, то получится 2-хзначное число, которое при сумме цифр равной 13 является наибольшим. Первая цифра числа больше последней в 4 раза. Сколько лет старику Хоттабычу?

4.  Завещание. Некто, умирая, оставил жену в ожидании ребёнка и сделал перед смертью такое замечание: в случае рождения сына отдать ему 2/3 имущества, а 1/3 – матери; : в случае рождения дочери отдать ей 1/3 имущества, а матери – 2/3 имущества. Вдова завещателя родила близнецов – мальчика и девочку. Как разделить имущество по завещанию?

5.  Бутылка и стакан вмещают столько же жидкости, сколько кувшин. Бутылка вмещает столько же, сколько стакан и пивная кружка. Три пивные кружки вмещают столько же, сколько два кувшина. Сколько стаканов жидкости вмещает одна пивная кружка?

6.  Книга. Одному школьнику подарили книгу. Сколько страниц в этой книге, если для нумерации её страниц потребовалось 2775 цифр?

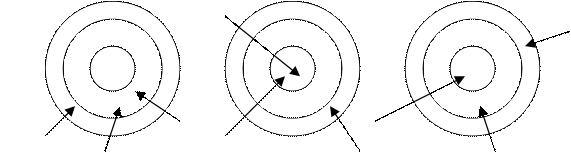
7.  Дартс. Играя в дартс, Женя трижды бросил по три дротика в мишень. Попадание дротика в определённый круг мишени оценивается соответствующим числом очков. В первый раз Женя получил в сумме 29 очков, во второй раз – 43 очка (см. рис.) Сколько очков получил Женя в третий раз?

Вспомним геометрию.

1.  Какое максимально возможное число внутренних углов, равных 90^о, может быть в шестиугольнике (не обязательно выпуклом)?

2.  Имеется 6 отрезков, длины которых 1см, 2 см, 3 см, 2001 см, 2002 см и 2003 см. Нужно выбрать 3 из этих отрезков так, чтобы из них можно было составить треугольник. Сколько различных треугольников при этом можно получить?

3.  В прямоугольнике ABCD точки P, Q, R и S являются серединами сторон AB, BC, CD и AD соответственно, а Т – середина отрезка RS. Какую часть от площади прямоугольника ABCD составляет площадь треугольника TQP?

3.Миша собрал из 42 одинаковых кубиков с ребром 1 см прямоугольный параллелепипед. Периметр основания параллелепипеда оказался равен 18 см. Какую высоту имеет построенный параллелепипед?

4.  На краях квадратного листа бумаги, разбитого на 25 клеток, отмечены точки A, B, C, D, E, M и N, как показано на рисунке. Найдите сумму углов MAN, MBN, MCN, MDN и MEN.

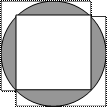
2.Два квадрата одного и того же размера покрывают круг радиуса 3 см, как показано на рисунке. Найдите площадь окрашенной части круга.

Весёлые задачи.

1.В окно с тротуара брошен камень со скоростью 5 м/с. Оцените, с какой скоростью он вылетит оттуда назад.

2.В одно ухо школьника влетит 20 слов в минуту, а из другого вылетит 10 слов в минуту. Найдите время, за которое школьник поумнеет.

3.С какой скоростью нужно орудовать вилкой, чтобы, пользуясь ею съесть полную порцию каши за две минуты?

1.  С какой высоты должен падать парашютист без парашюта, чтобы от него не осталось мокрого места?