Построение эмпирической кривой обеспеченности годового стока. Построение гидрографа среднемесячных расходов и потребления

    1 Построение эмпирической  кривой обеспеченности, то есть кривой распределения ежегодных вероятностей распределения, годового стока реки и подбор сглаживающей ее аналитической кривой.

1.1  Из задания заносят в графы 2 и 3 таблицы 1.1 данные о средних значениях расхода воды за каждый из указанный календарный год.

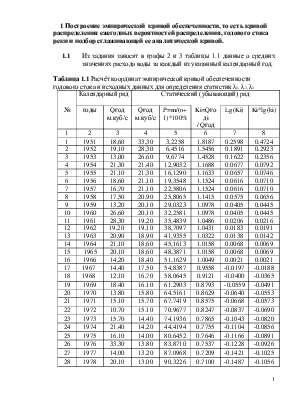
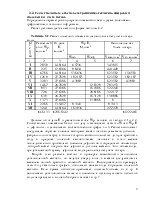
Таблица 1.1 Расчёт координат эмпирической кривой обеспеченности годового стока и исходных данных для определения статистик λ1, λ 2, λ3

549.3        549.3        1500             30         -0,4135      0,428

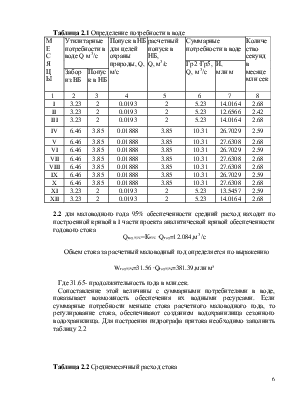
     1.2 Размещают в графу 4 значение годовых расходов воды в убывающем порядке от наибольшего к наименьшему. Строят многолетние гидрографыдля хронологического и убывающего рядов (приложение 1).

Находят сумму значений расходов всех n-членов убывающего ряда. Находят сумму значений расходов всех n-членов убывающего ряда и записывают внизу графы 4. Определяют значение первого параметра данного ряда и его среднеарифметическое

λ1 =Qгод=ΣQгод i/n

Выражают значение всех параметров убывающего ряда в модульных коэффициентах и записывают в графу 6

ki= Qгод i/ Qгод

Для контроля вычислений находят сумму значений ki, которая должна быть равна 30.

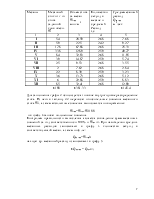
1.3 Выясняется, нет ли в составе данного ряда резко отклоняющихся членов не характерных для периода наблюдений с заданной продолжительностью или вследствие каких-то грубых ошибок. Для этого используются не параметрический критерий Диксона. Находим его значения для крайних членов выборки (наибольшее и наименьшее).

rmax=(k1-k3)/(k1-kn-2)=(1,8187-1,4528)/(1,8187-0,71)=0,33

rmin =(kn-2-kn)/(k3-kn)=(0,71-0,5844)/(1,4528-0,5844)=0,144 где k1 и k₃- значения модульных коэффициентов 1 и 3 ряда

kn   и kn-2 значения модульных коэффициентов последнего и третьего сзади членов ряда.

Если оба или одно из вычисленных значений (rmax и rmin) окажутся больше 0,457(при n=30), то гипотеза о однородности членов отвергается. Если они меньше 0,457 но больше 0,366 , то гипотеза сомнительна. Если эти значения меньше 0,366, то гипотеза принимается. В случае отклонения гипотезы, из ряда исключают неподходящий член. Проверяем на однородность ряд из оставшихся членов и при благоприятном исходе включанм в дальнейшую обработку. Так как rmax и rmin  меньше 0.366, то гипотеза принимается.

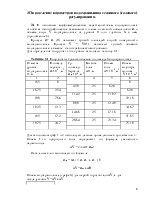
1.4 Значения ki всех членов ряда являются ординатами точек эмпирической кривой обеспеченности. Их абсцисса определяется:

Pi=mi/(n+1)*100% где Pi - обеспеченность рассм-го члена со значением ki,

mi - номер члена Pi Pi, в убывающем ряду,

ni - общее число членов.

Если обеспеченность Р<50% то речь идет об обеспеченности максимальной, гидрологической величины и повторяемость N определяю формуле:

N=100/P

Если обеспеченность Р >50% то речь идет об обеспеченности минимальной гидрологической величины и повторяемостьN определяется по формуле:

N=100/100-P

По полученным данным (Pi ki) наносятся точки эмпирической кривой (рис.1.1).Необходимо визуально убедится, что не осталось резко отклоняющихся точек свидетельствующих о неоднородности соответствующих членов.

Таблица 1.1- расчет координат эмпирической кривой обеспеченности годового стока реки и исходных данных для определения статистик (приложение 3).

    1.5 Для построения аналитической кривой обеспеченности 2 остальных ее параметра определяют рекомендуемым методом наибольшего правдоподобия, для этого вычисляют значения 2 и 3 логарифмических статистик:

λ1 =Σlgki(n-1)=-11,9915 

λ3=Σkilgki(n-1)=12,3192 

   По монограммам определяют значения параметров Сv и Cs аналитической кривой обеспеченности трехпараметрического гамма распределения.

Сv =σх/х= Σ(хi-х)/(n-1)x =  Σ(ki-1) /(n-1) 

Cs=M3/σх= Σ(хi-х)/(n-1)σх=Σ(ki-1)/(n-1) Сv   

1.6 Пользуясь таблицами координат кривых трехпараметрического гамма распределения и, прибегая к необходимой интерполяции, выписывают коэффициенты аналитической кривой соотношением Cs/ Сv наиболее близко соответствующим значениям параметров, установленных в пункте