Построение многолетнего гидрографа, эмпирической и аналитической кривых обеспеченности годового стока реки. Построение эмпирической и аналитической кривых обеспеченности годового стока реки

1. Построение многолетнего гидрографа, эмпирической и аналитической кривых обеспеченности годового стока реки

1.1  Построение многолетнего гидрографа

Для его построения используют данные, приведенные в задании по курсовому проектированию. Все расчеты при построении удобно свести в Таблицу 1 следующей формы:

Таблица 1– Расчетные значения для построения гидрографа

Пользуясь  результатам Таблицы 1 (графы 3 и 4) строят многолетний гидрограф годового стока реки, который представлен в виде двух ступенчатых графиков: для календарного и статистического рядов(рисунок 1 и 2).

1.2 Построение эмпирической и аналитической кривых обеспеченности годового стока реки

Для построения графиков обеспеченности годового стока реки используются статистические методы обработки многолетнего ряда наблюдений расходов воды.

1.2.1 Определение среднемноголетнего расхода воды и модульных коэффициентов

В Таблице 1 (графа 4) находят сумму значений всех n членов (их 30 в ряду наблюдений) убывающего ряда ∑Q_{год i}и записывают ее внизу графы 4.

Определяют первый параметр данного ряда – ее среднее значение за многолетний период:

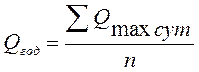, где Q_{год i} – средний расход воды за i-тый  календарный год;

n – общее число членов ряда.

.

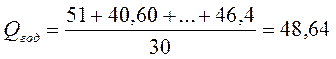Далее выражают значения всех параметров убывающего ряда в модульных коэффициентах (т.е. в долях от их среднего значения) К_i, результаты записываются в графу 6.

,

.

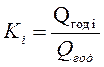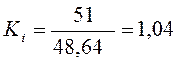Для контроля следует проверить сумму значений K_i. Она должна быть равна числу членов ряда n=30.

∑K_i=1,048+0,834+…+0,953=30

Проверка сошлась, следовательно вычисления выполнены верно.

1.2.2 Проверка однородности ряда наблюдений

В ходе проверки выявляется наличие в статистическом ряду наблюдений нерепрезентативных (т.е. резко отклоняющихся по величине) членов. Эти значения величин могут попасть в статистический ряд наблюдений в результате грубых ошибок или естественных обстоятельств, не характерных для периода наблюдений заданной продолжительности.

Для проверки используют непараметрический критерий Диксона. При этом находят его значения для крайних членов статистического ряда – наибольшего r_max и наименьшего r_min. Для n=30

,

,

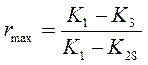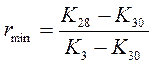В результате подстановки данных значений и вычисления получается:

,

,

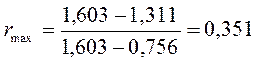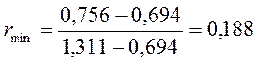Если результаты вычислений по приведенным формулам окажутся больше 0,457 (т.е. критериального значения однопроцентной значимости при n=30), то гипотеза об однородности членов ряда отвергается.

В данном случае значения меньше 0,366 и гипотеза принимается, и статистический ряд наблюдений полностью включают в дальнейшую обработку.

1.2.3 Построение эмпирической кривой обеспеченности годового стока реки

Эмпирическая кривая обеспеченности строится по значениям модульного коэффициента К_iи обеспеченности каждого рассматриваемого члена в ряду р_i. Значения К_i определены в графе 6  Таблицы 1, а обеспеченность р_i определяется по формуле:

р_i = 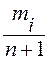^. 100% , где р_i  – обеспеченность рассматриваемого члена со значением К_i;

m_i   – номер члена К_i  в убывающем ряду;

n – общее число членов ряда.

р_i = 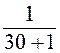^. 100% = 3,226.

По данным Таблицы 1 (графы 5 и 6) строится график эмпирической кривой обеспеченности.

На построенном графике точки резко не отклоняются от положения соседних, что свидетельствует о неоднородности соответствующих членов