
Задача 1в Построение эмпирических формул методом наименьших квадратов. Точечная квадратичная аппроксимация.
Постановка задачи. Данные об изменении нагрузки в одной точке в течение некоторого промежутка времени заданы в таблице:
|
t, ч |
15 |
18 |
21 |
24 |
27 |
30 |
33 |
36 |
39 |
42 |
|
H, кН |
4,5 |
5,2 |
5,8 |
6,3 |
7,0 |
7,7 |
8,3 |
8,8 |
9,5 |
10,0 |
Вывести эмпирическую формулу зависимости нагрузки от времени. Характер зависимости установить графически. Определить погрешность вычислений.
Решение: 1 По табличным данным зависимости строим корреляционное поле
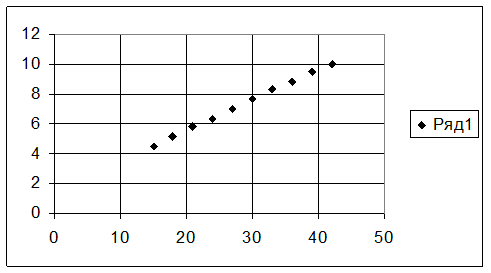
2 Согласно построенному графику принимаем, что зависимость между H и t носит параболический характер. Исходя из этого, эмпирическую формулу зависимости нагрузки от времени можно представить в виде аппроксимирующего многочлена первой степени Q(t) = a0 +a1t+ a2t2, где a0, a1 , a2 – коэффициенты уравнения, которые находим методом наименьших квадратов, решив систему нормальных уравнений:
![]()
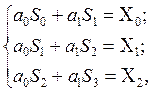
где
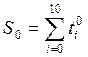 ;
;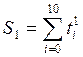 ;
;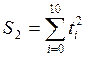 ;
;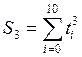
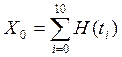 ;
;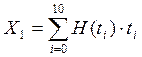 ;
;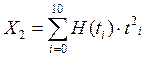 .
.
Составим таблицу:
|
i |
t0i |
t1i |
t2i |
Н(ti) |
Н(ti) t1i |
|
0 |
1 |
15 |
255 |
4,5 |
67,5 |
|
1 |
1 |
18 |
324 |
5,2 |
93,6 |
|
2 |
1 |
21 |
441 |
5,8 |
121,8 |
|
3 |
1 |
24 |
576 |
6,3 |
151,2 |
|
4 |
1 |
27 |
729 |
7 |
189 |
|
5 |
1 |
30 |
900 |
7,7 |
231 |
|
6 |
1 |
33 |
1089 |
8,3 |
273,9 |
|
7 |
1 |
36 |
1296 |
8,8 |
316,8 |
|
8 |
1 |
39 |
1521 |
9,5 |
370,5 |
|
9 |
1 |
42 |
1764 |
10 |
420 |
|
Σ |
10 |
285 |
8865 |
73,1 |
2235,3 |
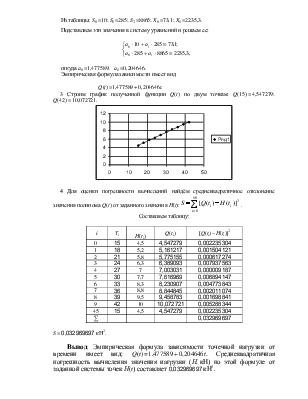
Из таблицы: S0 =10; S1 =285; S2 =8865; X0 =73,1; X1 =2235,3.
Подставляем эти значения в систему уравнений и решаем ее:
![]()
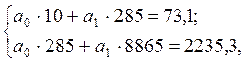
откуда a0 =1,477589; a1 =0,204646.
Эмпирическая формула зависимости имеет вид
Q(t) =1,477589 + 0,204646t.
3 Строим график полученной функции Q(t) по двум точкам: Q(15) = 4,547279; Q(42) = 10,072721.


4 Для оценки погрешности вычислений найдём
среднеквадратичное отклонение значения полинома Q(t) от заданного
значения Н(t): 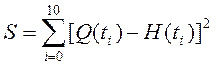 .
.
Составляем таблицу:
|
i |
Ti |
Н(ti) |
Q(ti) |
[Q(ti) – Н(ti)]2 |
|
0 |
15 |
4,5 |
4,547279 |
0,002235304 |
|
1 |
18 |
5,2 |
5,161217 |
0,001504121 |
|
2 |
21 |
5,8 |
5,775155 |
0,000617274 |
|
3 |
24 |
6,3 |
6,389093 |
0,007937563 |
|
4 |
27 |
7 |
7,003031 |
0,000009187 |
|
5 |
30 |
7,7 |
7,616969 |
0,006894147 |
|
6 |
33 |
8,3 |
8,230907 |
0,004773843 |
|
7 |
36 |
8,8 |
8,844845 |
0,002011074 |
|
8 |
39 |
9,5 |
9,458783 |
0,001698841 |
|
9 |
42 |
10 |
10,072721 |
0,005288344 |
|
45 |
15 |
4,5 |
4,547279 |
0,002235304 |
|
∑ |
0,032969697 |
S = 0,032969697 кН2.
Вывод: Эмпирическая формула зависимости точечной нагрузки от времени имеет вид: Q(t) =1,477589 + 0,204646t. Среднеквадратичная погрешность вычисления значения нагрузки (Н, кН) по этой формуле от заданной системы точек Н(t) составляет 0,032969697 кН2.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.