Напряжения в пространственном брусе

ЗАДАНИЕ НА РАСЧЕТНО – ГРАФИЧЕСКУЮ РАБОТУ

«НАПРЯЖЕНИЯ В ПРОСТРАНСТВЕННОМ БРУСЕ»

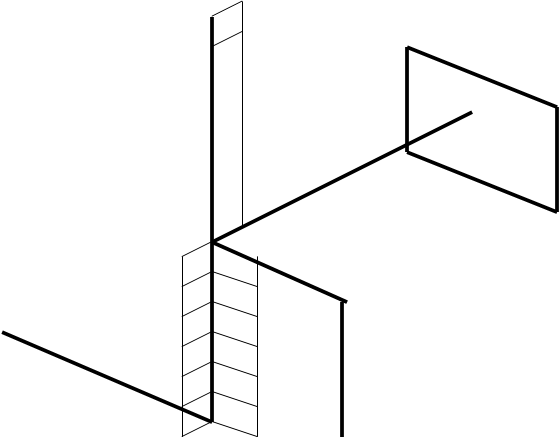
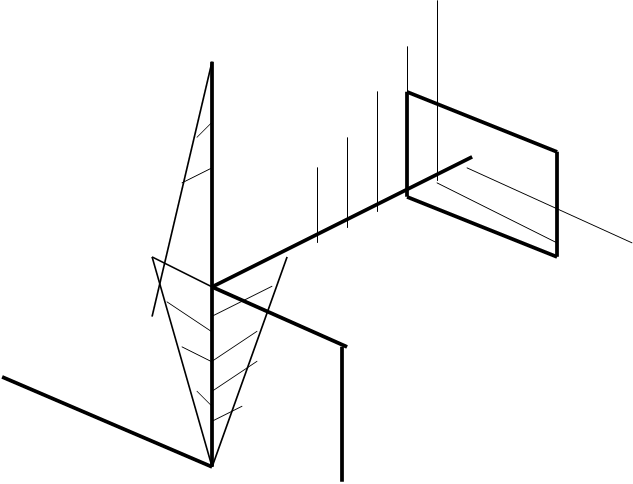
I.      В соответствии с исходными данными, соблюдая приемлемый масштаб, вычертить пространственный брус в аксонометрии. На схеме бруса показать заданную внешнюю нагрузку и записать её численные значения.

Таблица исходных данных:

F7	F4	F1	b	q1	h	F10	l	q2	m	d
19	-24	15	17	-7	30	58	0.8	-22	-7	12

II.     Построить эпюры всех внутренних усилий, указав на эпюрах знаки и численные значения характерных ординат. Произвести контроль эпюр в пределах каждого элемента бруса, в том числе и проверить равновесие всех узлов.

III.В соответствии с эпюрами внутренних усилий:

-  установить вид деформации для каждого элемента бруса 

-  наметить предполагаемые опасные сечения во всех элементах бруса.

IV.   В каждом предполагаемом опасном сечении:

-  показать все внутренние усилия в соответствии с эпюрами;

-  построить пространственные эпюры нормальных и касательных напряжений отдельно от каждого внутреннего усилия;

-  построить пространственную суммарную эпюру нормальных напряжений, показать нейтральную линию и записать max σ и

min σ;

-  вычислить max τ, используя эпюры касательных напряжений;

-  наметить точи, опасные по совместному действию нормальных и касательных напряжений; выделить в окрестности этих точек элементарные параллелепипеды, показать на их гранях нормальные и касательные напряжения и определить вид напряженного состояния (линейное, плоское или объемное); с учетом вида напряженного состояния вычислить  эквивалентные напряжения по одной, выбранной студентом из теории прочности.

 

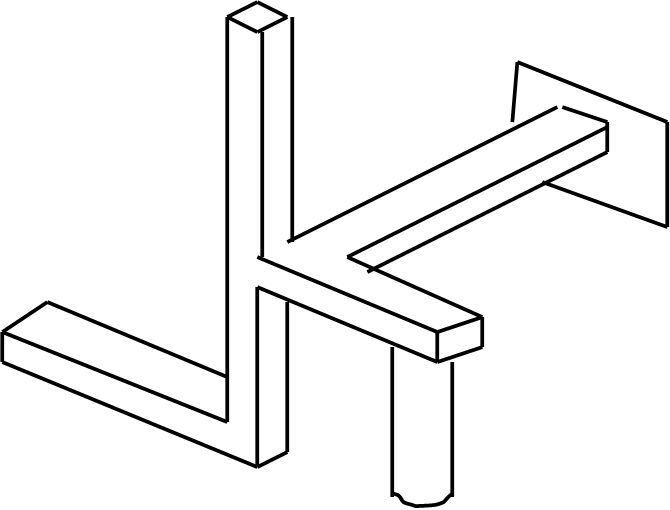
b                                                      2b

h                                                         2b

Рисунок 1.

d

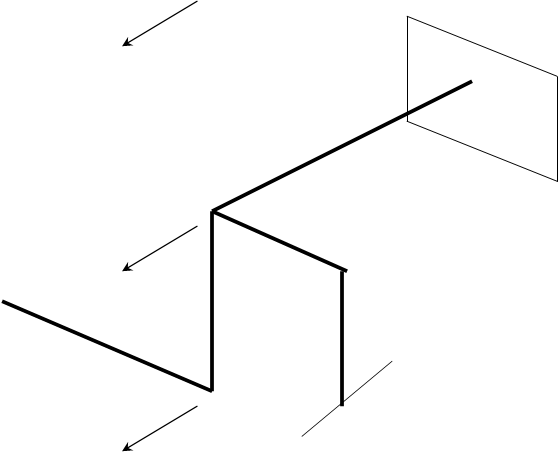
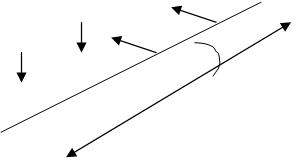
Сделаем схематический рисунок и расставим все силы действующие на      брус и обозначим буквами a,b,c,d,e,f узлы бруса.

                                                                  a

 

                                                    F₁

                                                                                q₂

 

                                                                                              q₁

d                            2l

                                                      F₁₀                                   e

F₄

b

 

c

f    m

F₇

 

 

Элемент ad: В этом стержне возникает одна поперечная сила Q=-F₁=-15 кH

Элемент bc: В этом стержне возникает одна продольная сила N=F₄=-24 кH

Элемент ef: Испытывает изгиб в вертикальной плоскости от m=-7 кН·м

Элемент ed:  внешний момент переносим из точки f в точку e и рассматриваем элемент de как  стержень замещенный в сечении  d . Элемент df испытывает деформацию кручения.

Элемент dc: Силу F₄ переносим в точку с , теперь рассматриваемый стержень dc нагружен двумя силами F₄ и F_7. В его сечении возникают поперечные силы  во взаимно перпендикулярных вертикальных плоскостях. 

Q₁=F₄=-24 кH;

Q₂=F₇=19 кH.

M₁=F₄·l=-24·0.8=19.2 кН·м

M₂=F₇·l=-19·0.8=15.2 кН·м

Элемент do: всю внешнюю нагрузку распложенную по одну сторону от сечения  d приводим к  центру тяжести сечения, и рассматриваем элемент dо как стержень защемленный  в сечении O.В его сечениях возникают:

Продольная сила N=F₁₀+F₇ +F₁=58+19+15=92 кН

Поперечная сила в горизонтальной плоскости  Q= F₄=-24 кН

Крутящий момент    М_к= F₄·l=-24·0.8=19.2 кН·м

Изгибающий момент  в вертикальной плоскости  М_d1= F₇·l–F₁·l =-15.2-12=3.2 кН·м

Изгибающий момент  в горизонтальной плоскости  М_d2= m =-7 кН·м

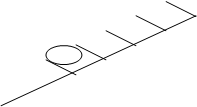
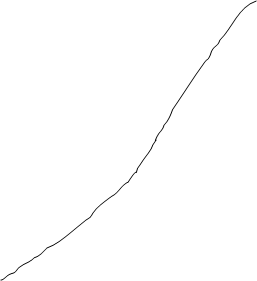
Строим эпюры напряжений.

M_к(кН·м)                                                     N(кН)

 

                                                                                                       92

 

                                            19,2

                                                                            24

    

7

 

Q(кН)

 

                                                         15                            -22

 

                                                                   

 

                                                                                               -31

                                                                           

 

19          -24

M(кН·м)

                                                                                         -14,4

 

                                                     3,2

 

                                   19,2                                                                                                    -12,6

                                                                       -7

15,2                                         

В соответствии с эпюрами внутренних усилий установим вид деформации для каждого элемента бруса.

Брус bc испытывает растяжение;

Брус ef испытывает кручение;

Брус ed испытывает крутящий момент;

Брус cd испытывает поперечный изгиб;

Брус ad испытывает поперечный изгиб;

Брус do испытывает растяжение крутящий момент и поперечный изгиб;