Модели сетевого планирования и управления

Лекция № 4-2.  МОДЕЛИ СЕТЕВОГО ПЛАНИРОВАНИЯ И УПРАВЛЕНИЯ

Модели сетевого планирования и управления (СПУ) широко используются на промышленных предприятиях и организациях, в строительстве для планирования сложных строительных работ и производства крупных изделий, проектирования современных агрегатов, проведения научных разработок. Сетевое планирование позволяет наглядно представить взаимосвязь и взаимозависимость между отдельными элементами систем, определить те работы, которые лимитируют выполнение других работ и всего плана в целом.

В основе методов СПУ лежит графическое представление комплекса работ (проекта) в виде сетевого графика.

Сетевой график - это ориентированный граф без контуров, дуги которого имеют одну или несколько числовых характеристик. Дугами изображаются работы, а вершинами – события.

Работа - любой трудовой процесс или действие, сопровождающееся затратами времени и ресурсов ( обозн. стрелками). Цифры на стрелках – это продолжительность работ.

Виды работ:

·  активная (действительная), требующая затрат времени и ресурсов (например, подвоз и укладка рельсов);

·  пассивная (ожидание), требующая затрат только времени (например, естественная сушка материалов или затвердение бетона);

·  фиктивная, не требующая никаких затрат и указывающей лишь последовательность событий (обозн. пунктирными стрелками   - - ->).

Событие не является процессом, а обозначает лишь факт окончания каких-то работ и начало новых.

Виды событий:  исходное, завершающее, промежуточое.

Событие, с которого начинается выполнение проекта, является исходным, оно не имеет предшествующих работ. Событие, которое констатирует факт завершения проекта, называется завершающим, оно не имеет последующих работ. Таким образом, каждое событие (за исключением исходного) всегда обозначает окончание одной или нескольких работ, входящих в него, и начало одной или нескольких работ (за исключением завершающего), выходящих из него.

Событие совершается тогда, когда закончены все предшествующие ему работы. Оно становится предпосылкой для начала следующих за ним работ.

Путем на сетевом графике называется любая последовательность событий и работ. Путь называется полным, если он соединяет исходное событие с завершающим.

Продолжительность любого пути равна сумме длительностей лежащих на нем работ.

Полный путь называется критическим, если он имеет наибольшую продолжительность во времени (таких путей может быть несколько).

Работы, лежащие на критическом пути, называются критическими. Суммарная продолжительность работ, принадлежащих критическому пути, определяет время выполнения комплекса в целом.

РАСЧЕТ ПАРАМЕТРОВ СЕТЕВОГО ГРАФИКА

При оптимальном планировании комплекса работ на сетевой модели используют ряд параметров. К таким параметрам относятся: длительность выполнения каждой работы, сроки наступления событий и резервы времени отдельных работ.

Для выявления резервов времени у работ рассчитывают сроки наступления событий. Обозначим через t_ij – длительность работы а_ij, исходящей из i -события и завершающейся j- событием.

Прежде чем представить проект сетевым графиком, составляют перечень работ, оценивают их длительность, устанавливают последовательность работ (какие работы обязательно должны быть закончены, чтобы могли начаться те или иные следующие) и определяют события.

На практике получил широкое применение четырехсекторный графический способ расчета ранних и поздних сроков свершения события.

i - номер события

t_р(i) - ранний срок свершения события i.

t_п(i) - поздний срок свершения события i.

R(i) - резерв времени для данного события

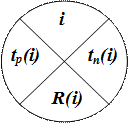
Ранний срок t_p(j) свершения события j -это срок, необходимый для выполнения всех работ, предшествующих этому событию:

Для исходного события I и завершающего S предполагается, что   t_p(I)=0;     t_p(S) = t_кр.

Поздний срок t_п(i) свершения события i- это такой предельный срок, после которого остается столько времени, сколько требуется для выполнения всех работ, следующих за этим событием:

Для завершающего события S предполагается, что      t_п(S)=t_р(S)=t_кр.

Резерв времени R(i) события i показывает, на какой предельно допустимый срок может задержаться свершение события i без нарушения срока свершения завершающего события S:        

Построение сетевого графика.

1). Вычисляемt_п(i) перемещаясь по сети от события I к событию S в порядке возрастания номеров. t_p(I)=0;     t_p(S) = t_кр

2). Вычисляем. t_п(i) перемещаясь по сети от события S к событию I в порядке убывания номеров. T_Ls = T_Es; T_L1 = T_E1 = 0

3) Вычисляем Ri

4) Строим критический путь и определим его длину (критическое время) - от последнего события сети.

А) Выбирают все события с нулевым резервом R(i) = 0 (события и работы, лежащие на критическом пути, не имеют резервов времени)