Определение теплоемкости методом наименьших квадратов с использованием языка Си

Цель: методом наименьших квадратов с использованием языка Си найти теплоемкость.

1.  Задание на курсовую работу

Опытным путем найдены истинной теплоемкости кислорода  при постоянном давлении , при соответствующей температуре.

Необходимо найти методом наименьших квадратов две приближающие функции: линейную  и логарифмическую  и полученные приближения сравнить, то есть выяснить, какое из данных приближений описывает процесс лучше. На основе полученных результатов построить графики обеих функций и нанести на них точки, соответствующие исходным данным.

2. Исходные данные

№ варианта
7	29.2752		33.5501	35.9123

Математическая модель:

Для приближения результатов опыта функцией вида   необходимо разрешить систему уравнений относительно а и b:

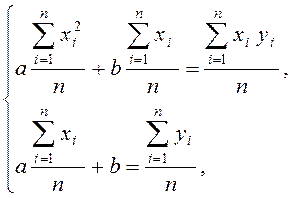                                                         (1)

Для приближения функцией вида: , то в исходной таблице значений нужно  заменить значениями, например, , затем вновь разрешить линейную систему уравнений относительно а1 и b1:

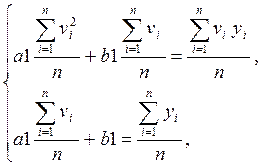                                                              (2)

Для того, чтобы убедиться какое из приближений оказалось лучшим, нужно вычислить:

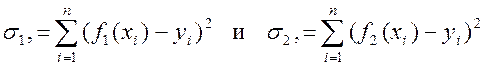,              и, если ,  то наилучшим из двух будет второе приближение.

Введём следующие обозначения:

x=t, =m

,, ,

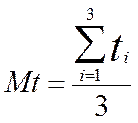
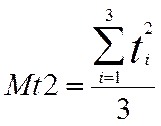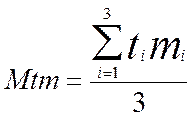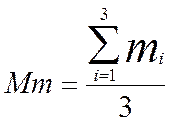
Так как ln0 не существует, заменим t=0 на близкое к нулю значение t=0.0001

Выразим из системы (1) а и b для функции вида

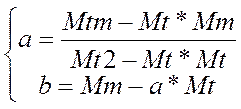
Выразим из системы (2) а1 и b1 для функции вида

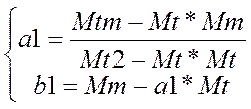
3.Результаты расчетов:

a=0.006637           a1=1.043464

b=29.593981        b1=2.129602

s1=0.101624

s2=1896.619385

4.Текст программы

#include <stdio.h>

#include <conio.h>

#include <math.h>

void dim(float w, float z);

void main()

{clrscr();

float T[3]={ 0.0001, 500, 1000};

float M[3]={ 29.2752, 33.5501, 35.9123};

float Mt,Mt2, Mtm, Mm, Lt, Lt2, Ltm, Lm, a, b, a1, b1, s1, s2;

int i;

for (i=0; i<3; i++)

{ Mt+=T[i]/3;

Mt2+=pow(T[i],2)/3;

Mtm+=(T[i]*M[i])/3;

Mm+=M[i]/3;

Lt+=(log(T[i]))/3;

Lt2+=(pow(log(T[i]),2))/3;

Ltm+=(log(T[i])*M[i])/3;

Lm+=(log(M[i]))/3;

a=(Mtm-Mt*Mm)/(Mt2-Mt*Mt);

b=Mm-a*Mt;

a1=(Ltm-Lt*Lm)/(Lt2-Lt*Lt);

b1=Lm-a1*Lt;

s1+=pow(a*T[i]+b-M[i],2);

s2+=pow(a1*log(T[i])+b1-M[i],2);

dim(s1,s2);

printf("\n%f\n%f\n%f\n%f\n%f\n%f",a,b,a1,b1,s1,s2);

}}

void dim(float w, float z)

{

if(w<z)

printf ("\n lineynaya funkciya priblizhaet luchshe");

else

printf ("\n logarifmicheskaya funkciya priblizhaet luchshe");

getch();}

5.Список использованной литературы:

1.  Подбельский В.В., Фомин С.С. Программирование на Си: Учеб. Пособие. – 2-е доп. изд. – М.: Финансы и статистика, 2000. 600 с.: ил.

2.  Волков Е.А. Численные методы. 3-е изд. испр. – СПб.: Издательство “Лань”, 2004. -248 с.

6.Содержание:

1. Задание на курсовую                                                                               1

2. Исходные данные и математическая модель                                          1

3. Результаты расчетов                                                                                2

4. Текст программы                                                                                     3

5. Список использованной литературы                                                      4

6. Содержание                                                                                                5