Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ ИНСТИТУТ ЦВЕТНЫХ МЕТАЛЛОВ И ЗОЛОТА»
Институт ИМ
Кафедра АПП
Дисциплина Программирование
Группа АМЦ 03-1
Отчёт
По лабораторной работе №2
«Вычисление площади заданной ограниченной области»
Преподаватель _____________ Ратушняк В.С.
(подпись, дата)
Разработал студент _____________ Вульфович А.А.
(подпись, дата)
Красноярск, 2007 г.
Задание.
В варианте лабораторной работы дана область на координатной плоскости, ограниченная определенными функциями, заданными в различной форме. Задание состоит в следующем:
1. Написать программу расчета площади фигуры на рисунке, двумя способами:
а – последовательного интегрирования (методом трапеций)
б – Монте-Карло.
2. Дополнить алгоритм вычисления площади методом Монте-Карло графической иллюстрацией.
Работа:
Дана функция:
y(x)=.2785*(х+6)^3-3.7953*(х+6)^2+15.99*(х+6)-20.636+15.99*(х+6)-20.636
Текстпрограммы.
#include<iostream.h>
#include <graphics.h>
#include <fstream.h>
#include <conio.h>
#include <stdlib.h>
#include <stdio.h>
#include <math.h>
void main(void)
{int dr=DETECT, mod=1; initgraph (&dr,&mod,"");setcolor(15);
int k=75;
for (double i=-2;i<5;i++)
{if (i==0)setcolor(15);else setcolor(8); line (400-4*k,300-k*i,400+2*k,300-k*i);
gotoxy(51,20-i*k/16);cout << i;
}
for (i=-4;i<3;i++)
{if (i==0)setcolor(15);else setcolor(8);line (400+k*i,300-4*k,400+k*i,300+2*k);
if (i != 0){gotoxy(51+i*k/8,20);cout << i;}
}
gotoxy(51+2*k/8,20);cout << "X";
gotoxy(51,20-4*k/16);cout << "Y";
double a=1e-4/2;
double x,s=0;
double y1(double),y2(double),y3(double),y4(double);
double ymin,ymax;
for (x=-4;x<2;x=x+a)
{ymax=y1(x);ymin=y4(x);
if(y4(x)>=y1(x)){ymax=y4(x);ymin=y1(x);}
if(y2(x)<=y4(x)){ymax=y2(x);}
if(y3(x)>=y1(x)){ymin=y3(x);}
if(y1(x)<4)putpixel(x*k+400,300-y1(x)*k,3);
if(y2(x)<4)putpixel(x*k+400,300-y2(x)*k,2);
if(y3(x)>-2)putpixel(x*k+400,300-y3(x)*k,9);
if (y4(x)<4&&x<0)putpixel(x*k+400,300-y4(x)*k,4);
if (x>-3.331&&x<1.485){setcolor(13);line(x*k+400,300-ymax*k,400+x*k,300-ymin*k);s=s+a*(ymax-ymin+0.03);}}
gotoxy (20,1);cout <<"s1=" << s;
getch();
getch();
int color=0;
double N=1e6*2,ty=0,tn=0,y;
for (i=0;i<N;i++)
{x=((random(1e4)/1e4)*5.2-3.5)*k+400;
y=((random(1e4)/1e4)*5-1.5)*-k+300;
color=getpixel(x,y);
if (color==13 || color==14)
{putpixel(x,y,14);ty++;}
else
{putpixel(x,y,8);tn++;}
s=26*ty/N;
}
gotoxy (35,1);cout << "s2="<< s;
getch();
getch();
}
double y1(double x){return 0.2785*pow(x+6,3)-3.7953*pow(x+6,2)+15.99*(x+6)-20.636;}
double y2(double x){return 1+pow(x,2);}
double y3(double x){return -1-pow(x,2);}
double y4(double x){if (x<0){return -1/x;}
else {return y2(x);};}
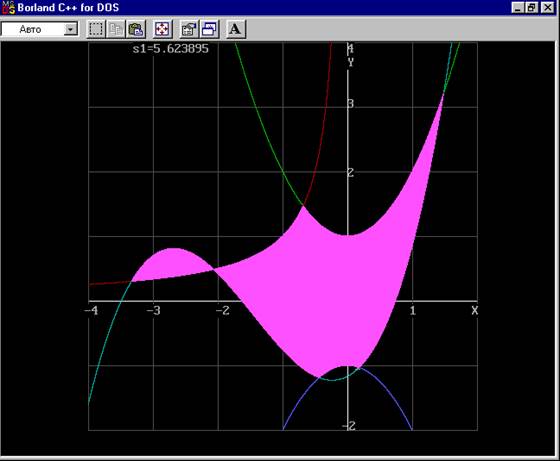
Рисунок1 – площадь найденная методом трапеций.
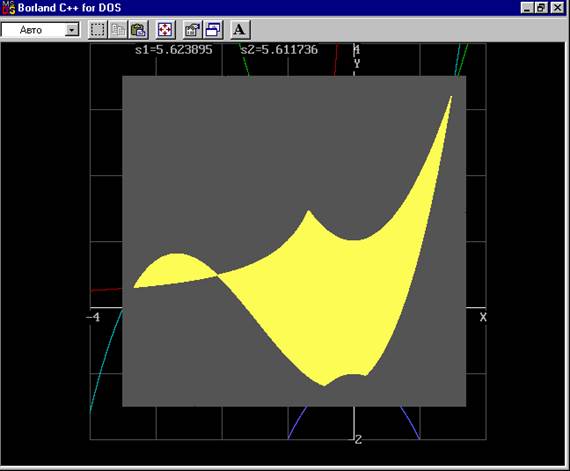
Рисунок2 – площадь найденная методом Монте-карло.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.