Классы ВМ:
1) метод эквивалентных преобразований (позволяет заменить исходную задачу к другой имеющей тоже решение);
2) методы аппроксимации (позволяет приблизить решение задачи к исходной, при этом возникает погрешность аппроксимации);
3) прямые (этот метод называется точным);
4) итерационные (основаны на построении последующего приближения к решению задач)
Однотипный набор действий с использованием найденных ранее приближении называется итерацией.
5) статистических испытаний (Монте-Карло), эти методы основных случайных величин и построений статистических оценок решения задач.
10. Вычислительный алгоритм (ВА) – точное предписание действий над входными данными, задающими вычислительный процесс, направленный на преобразование произвольных входных данных в полностью определенный этими входными данными результат.
ВА состоит из двух частей, абстрактной (запись на языке математики) и программной (на языке программирования).
Требования к ВА:
1) Корректность
2) Хорошая обусловленность
Требования к абстрактному ВА:
1) Экономичность (максимальная быстрота исполнения, определяется числом элементарных операций необходимых для вычисления алгоритма);
2) Точность;
3) Экономия памяти;
4) Простота;
Требование к программному ВА:
1) Надежность (не содержит ошибок и вычисляет именно, тот результат для которого предназначен);
2) Работоспособность;
3) Переносимость (программа может работать на различных ЭВМ без изменений или с не значит изменениями);
4) Поддерживаемость (легкость модификации программы);
5) Простота в использование.
11. ![]()
![]() - задана не линейная функция
- задана не линейная функция
![]() - неизвестная величина
- неизвестная величина
![]() - параметры задачи
- параметры задачи
Основные этапы решения:
1) Локализация (отделение корней);
2) Итерационное уточнение корней.
Локализация корней – нахождение таких интервалов изменения переменной ![]() , где расположен только один корень. О наличии на отрезке
, где расположен только один корень. О наличии на отрезке ![]() корня судят по перемени знака функции на концах
отрезка. Основанием для применения указанного способа служат две теоремы
математического анализа.
корня судят по перемени знака функции на концах
отрезка. Основанием для применения указанного способа служат две теоремы
математического анализа.
Теорема 1. Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]()
Теорема 2. Корень уравнения ![]() , будет единственным, если производная
, будет единственным, если производная ![]() существует и сохраняет знак внутри отрезка
существует и сохраняет знак внутри отрезка ![]() .
.
На втором этапе решения задачи производится уточнение отдельных корней т.е находятся значения корней с заданной точностью.
15. Метод простых итерации –
основан на преобразовании уравнения ![]() к виду
к виду ![]() ,
, ![]() - итерационная функция.
- итерационная функция.
Задавая произвольно значение ![]() и подставляя его в итерационную функцию получаем
значение
и подставляя его в итерационную функцию получаем
значение ![]() .
.
![]()
![]()
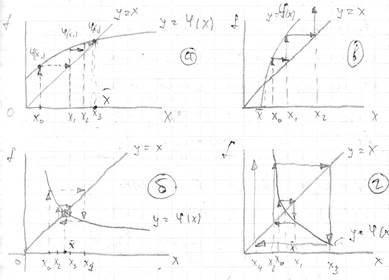
Метод простых итерации
является одношаговым. К корнями ![]() уравнение
уравнение ![]() является абсцисса точки пересечения графика двух
функций (рис.2).
является абсцисса точки пересечения графика двух
функций (рис.2).
![]()
![]()
а, б – односторонние и
двухсторонние процессы сходящиеся. ![]()
в, г - односторонние и
двухсторонние расходящиеся процессы. ![]()
19. Итерационные методы
решения СЛАУ. Якоби. Для использования методов простых итераций при решении
СЛАУ необходимо предварительно исходную систему вида ![]() преобразовать к виду
преобразовать к виду ![]() .
.
![]()
![]()
![]()
…………………………………
![]()
![]()
Затем задаются начальные приближения всех неизвестных величин
![]()
Критерием окончания расчета
является ![]()
Если при расчете ![]() для неизвестных с номерами
для неизвестных с номерами ![]() подставлять не значения
подставлять не значения ![]() , а значения
, а значения ![]() уже найденное на данном шаге приближения расчет будет
сходиться быстрее, такой метод называется методом Зейделя. Методы ориентированы
на решения разных классов систем, метод Якоби на системы с матрицами близкими к
диагональным, а метод Зейделя на систему с матрицами нижним треугольным.
уже найденное на данном шаге приближения расчет будет
сходиться быстрее, такой метод называется методом Зейделя. Методы ориентированы
на решения разных классов систем, метод Якоби на системы с матрицами близкими к
диагональным, а метод Зейделя на систему с матрицами нижним треугольным.
«+»: Простота программной реализации и отсутствие необходимости в памяти ЭВМ всех коэффициентов матрицы.
«-»: трудность получения оценок вероятности и скорости их сходимости.
21. (рис.3)
![]()
![]()
если первообразную функции ![]() от функции
от функции ![]() можно выразить через известные функции, то для
вычисления интеграла можно использовать формулу Ньютона-Лейбница.
можно выразить через известные функции, то для
вычисления интеграла можно использовать формулу Ньютона-Лейбница.
![]()
![]()
![]()
S– приближенное значение интеграла
R– погрешность вычисления интеграла
Методы численного интегрирования делятся на 3 группы:
1) Метод Ньютона-Котеса, основан на полиномиальной аппроксимации (методы прямоугольников, трапеций);
2) Сплайновый метод. Подынтегральная функция заменяется на сплайны представляет собой кусочный полином;
3) Наивысшей алгебраической точности (метод Гаусса-Кристоффеля) в этой группе методов используются неравноценные узлы расположенные по алгоритму обеспечивающие минимальную погрешность интегрирования.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.