11.
Сделать замену 
и выполнить по действиям.
12.
Очевидно, 
является корнем и левой части равенства.
Разделить многочлен на 
и приравнять кубические
многочлены.
13.
Из равенства 
.
14. Из уравнения выразить x через n и решить согласно условию.
15. Исследовать уравнение на наличие решения в зависимости от параметра m.
16. Записать условие, при котором система линейных уравнений имеет бесчисленное множество решений, откуда найти значение параметра.
17. Записать условие, при котором система линейных уравнений не имеет решения, откуда найти значение параметра.
18. Записать условие, при котором система линейных уравнений имеет единственное решение, откуда найти значение параметра.
19.
Неравенство 
равносильно объединению двух неравенств 1)
2) 
.
20. Решить методом интервалов.
Контрольная работа №2
1. Сгруппировать первую скобку с последней, вторую с
третьей и заменить, 
.
2. Сгруппировать первую скобку с последней, вторую с
третьей, Вынести из каждой скобки х и поделить обе части уравнения на 
. Заменить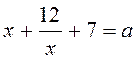 
.
3.
Обозначить 
.
4.
Умножим обе части уравнения на 
, обозначить 
.
5.
Обозначить 
,
решить, сделать обратную замену и проверку.
6.
Обозначить 
,решить, сделать обратную замену и проверку.
7. Приравнять к нулю каждый множитель, решить полученные уравнения и сделать проверку.
8. Возвести обе части уравнения в квадрат и сделать проверку.
9.
х=2 не является корнем
уравнения, т.к. не подходит по ОДЗ. Разделить обе части уравнения на 
,решить полученное уравнение.
10. Возвести обе части уравнения в квадрат, упростить и снова возвести в квадрат, сделать проверку.
11.
, 
.
12. Аналогично заданию 11.
13. Разделить обе части первого уравнения на 
, заменить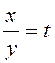 
,
решить, выразить х через y и подставить во второе уравнение.
14, 15. Решить методом интервалов.
16. 
, 
и 
.
17. 
, 
или 
.
18.
Уравнение имеет два различных
действительных корня, если 
и D>0.
19. График данной квадратичной функции лежит ниже оси Ох при любых значениях х, если D<0.
20. Использовать теорему Виета.
21. Раскрыть модуль, получить два уравнения. Чтобы исходное уравнение имело четыре различных корня, необходимо, чтобы данные уравнения имели по два различных корня, т.е. D >0. Очень хорошо решается графически.
22. Приравнять каждый множитель к нулю и решить. Уравнение имеет одно решение, если оба найденных корня совпадают или первый корень не подходит по ОДЗ.
Контрольная работа №3
1. Применить формулу суммы кубов.
2. Использовать формулы приведения.
3. Заменить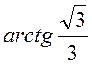 
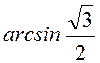на 
, 
на 
.
4. Преобразовать данное выражение.
5. Применить формулу синуса двойного угла.
6. Выразить синус половинного угла через косинус целого.
7. Опустить период и заменить косинус на синус дополнительного угла.
8. Опустить период и вычислить.
9. Опустить период и заменить синус на косинус дополнительного угла.
10. Применить формулу тангенса разности углов.
11.
Умножить и разделить выражение на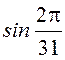 
.
12.
Использовать формулу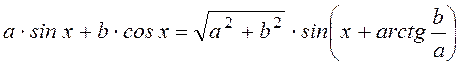 
.
13. Преобразовать подкоренное выражение к одной функции и оценить.
14. Найти период каждого слагаемого и как наименьшее общее кратное найти период данной функции.
15. Решить уравнение и сделать отбор корней.
16.
Преобразовать к квадратному уравнению и
взять дискриминант 
.
17.
Решить уравнение и выбрать корни,
принадлежащие отрезку 
.
18.
Ввести переменную 
и решить неравенство методом интервалов.
19.
Найти область определения, затем корни,
принадлежащие 
.
20.
Свести уравнение к квадратному и взять
дискриминант .
21.
Использовать область определения
функции 
.
22. Понизить степень и ввести новую переменную.
23. Выделить параметр a и найти область изменения функции, стоящей в левой части уравнения.
24. Решение аналогичное № 23.
25. Определить, какой четверти принадлежит заданный отрезок. Найти наибольшее значение функции и значение функции на концах отрезка.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.