30. Мембранные гидроцилиндры
30.1. Устройство и принцип действия
Конструктивно мембранный гидравлический (или пневматический) цилиндр имеет защемленное по периферии круглое эластичное кольцо, связанное по центру с выходной нагрузкой (рис. 7.11, а). Как правило, это кольцо имеет жесткий центр а диаметром d равный 0,75– 0,85 диаметра D по которому кольцо защемлено в корпусе.
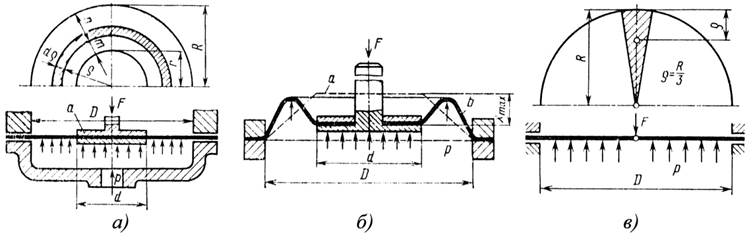
Рис. 7.11. – Схемы мембранного гидроцилиндра с мембраной плоского (а) и гофрированного (б) типов и без жесткого центра (в)
Упругая часть мембраны выполняется плоской (рис. 7.11, а) или гофрированной (рис. 7.11, б). Первая конструктивно проще второй, но плоская мембрана допускает значительно меньший ход центра в сравнении с гофрированными или тарельчатыми.
30.2. Усилие на жестком центре мембраны
Важным параметром мембранного гидроцилиндра является эффективная площадь мембраны – этоплощадь, величина которой умноженная на перепад давления, действующий на мембрану, определяет усилие, развиваемое на ее центре. Эта площадь является переменной величиной и ее расчет производят по приближенным формулам при допущении малых прогибов с последующей экспериментальной проверкой.
Площадь мембраны немеющей жесткого центра (рис. 7.11, в) можно условно разбить на ряд элементарных равнобедренных треугольников, с вершинами в центре мембраны и основаниями – у контура ее закрепления. Равнодействующая сила давления рабочей среды на каждый треугольник приложена на расстоянии 1/3 высоты треугольника от его основания. При этом опорная реакция элементарного треугольника площадью F0 будет обратно пропорциональна расстоянию от опоры до точки приложения равнодействующей.
Следовательно, эффективная площадь мембраны и усилие F, передаваемое на опору круглой мембраной без жесткого центра, закрепленной по внешнему контуру определится по формуле:
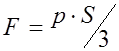 и
и 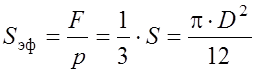 , где р
– избыточное давление под мембраной;
, где р
– избыточное давление под мембраной;
S – общая площадь мембраны по диаметру D закрепления контура в корпусе. Остальная часть площади мембраны ΔS = S - Sэф в передаче усилия на центральную опору не участвует.
Для увеличения полезного усилия мембраны в ее центре обычно устанавливают жесткую опору, образующую жесткий центр диаметром d (рис. 7.11, а). Расчет величины полезного усилия и эффективной площади производим предполагая, что мембранное полотно обладает совершенной эластичностью, а прогиб мембраны в центре равен нулю.
Выделим на рабочей поверхности
плоского мембранного кольца элементарную кольцевую площадь ![]() , удаленную от центра мембраны на
расстояние
, удаленную от центра мембраны на
расстояние ![]() (рис. 7.11, а). Усилие давления
жидкости на эту площадь будет передаваться на подвижный в осевом направлении
жесткий центр и неподвижные шайбы (корпус) наружного защемления и определится по
формуле:
(рис. 7.11, а). Усилие давления
жидкости на эту площадь будет передаваться на подвижный в осевом направлении
жесткий центр и неподвижные шайбы (корпус) наружного защемления и определится по
формуле:
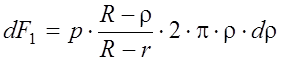 , где r
и R–
радиусы жесткого центра и окружности защемления мембраны в корпусе.
, где r
и R–
радиусы жесткого центра и окружности защемления мембраны в корпусе.
Следовательно, усилие, передаваемое на жесткий центр от рабочего участка мембранного полотна (без учета жесткого центра), после интегрирования и преобразования определится по формуле:
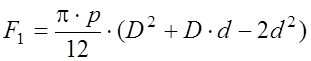 , где d и D – диаметр жесткого
центра и диаметр закрепления мембраны в корпусе.
, где d и D – диаметр жесткого
центра и диаметр закрепления мембраны в корпусе.
Давление среды, которое действует на полотно мембраны, будет действовать также и на жесткий центр, развивая усилие:
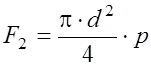 .
.
Следовательно, полное усилие мембраны будет равно:
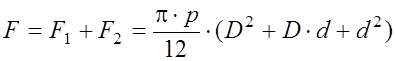 .
.
30.3. Зависимость эффективной площади мембраны от перепада
давления
Второй по значимости причиной изменения эффективной площади мембраны и, соответственно, нарушения стабильности их характеристик является изменение перепада давления. Зависимость эффективной площади мембран от перепада давления в основном обусловлена деформацией мембранного полотна под действием сил натяжения, определяемых перепадом давления.
При нагружении эластичных мембран перепадом давления они приобретают заметную жесткость. С увеличением перепада давления жесткость мембран повышается.
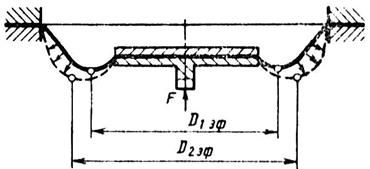
Рис. 7.12. – Схема действия на мембрану давления жидкости
На рис. 7.12 показана гибкая мембрана, находящаяся под некоторым малым давлением (сплошная линия). Эффективная ее площадь определяется для данного положения жесткого центра по формуле:
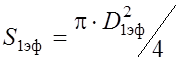 .
.
При повышении давления при неизменном положении жесткого центра упругая поверхность мембраны примет форму, показанную штриховой линией. В соответствии с этим эффективная площадь мембраны увеличится и определится по формуле:
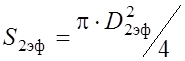 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.