Задания компьютерного практикума по курсу «Информатика» (2 семестр)
Задания по лабораторному практикуму достаточно сложны и требуют времени, к тому же выделяемого компьютерного времени тоже мало, поэтому не тратьте его на игрушки, а подойдите к курсу серьезно. На занятия приходите с готовыми программами, написанными на листочке, чтобы оставалось только ввести их в компьютер и проверить работоспособность (опять же из-за дефицита времени). Учтите В ИЮНЕ ПРЕПОДАВАТЕЛЬ ОЧЕНЬ ЗАНЯТ И НЕ УСПЕВШИЕ БУДУТ СДАВАТЬ В СЕНТЯБРЕ.
Соответствие выполненной работы и задания будет строго проверятся.
а) Составьте программу, решающую систему линейных уравнений n-го порядка по методу Жордана-Гаусса. Пользователь задает порядок системы, коэффициенты системы. В отчете привести блок-схему программы, текст программы с результатами ее работы.
б) Составьте программу, решающую систему линейных уравнений 3-го порядка по методу итераций. Пользователь задает коэффициенты системы. Предусмотреть защиту от расходящегося процесса. В отчете привести блок-схему программы, текст программы с результатами ее работы.
в) Составьте программу, решающую систему линейных уравнений 3-го порядка по методу Зейделя. Пользователь задает коэффициенты системы. Предусмотреть защиту от расходящегося процесса. В отчете привести блок-схему программы, текст программы с результатами ее работы.
1) Дифференциальное уравнение горизонтального полета самолета:
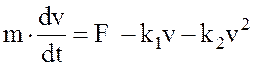 , где m - масса самолета; v - скорость
самолета; F - сила тяги двигателей;
, где m - масса самолета; v - скорость
самолета; F - сила тяги двигателей; ![]() -
коэффициенты аэродинамического сопротивления.
-
коэффициенты аэродинамического сопротивления.
Составить программу, в результате которой на экране выводится зависимость скорости от времени v(t). Предусмотреть возможность моделирования полета самолета неограниченное время. По желанию пользователя моделирование может быть остановлено для изменения силы тяги двигателей F, и массы m, а затем снова продолжено. Остальные величины считаются постоянными. Оси графиков градуируются. В отчете привести блок-схему программы, текст программы с результатами ее работы (графики, не менее 3).
2) Аэросани двигаются по пресеченной местности. Тяга воздушного винта F, масса саней m, коэффициент трения m, угол наклона склона к горизонту a. Дифференциальное уравнение выглядит:
![]()
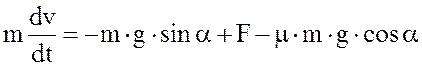
Составить программу, в результате которой на экране выводится зависимость скорости от времени v(t). Предусмотреть возможность моделирования движения аэросаней неограниченное время. По желанию пользователя моделирование может быть остановлено для изменения тяги воздушного винта F и угла наклона склона к горизонту a (угол может быть отрицательным при движении под гору), а затем снова продолжено. Остальные величины считаются постоянными. Оси графиков градуируются. В отчете привести блок-схему программы, текст программы с результатами ее работы (графики, не менее 3).
3) Пылинка массой m и зарядом q помещена в плоский конденсатор с расстоянием между обкладками d и расположенный горизонтально. Конденсатор подключен к синусоидальному напряжению Um· sin(wt), где Um – амплитуда, w - циклическая частота, причем w=2pf ; f – частота сети равная 50 Гц. Напряжение может меняться по амплитуде Um пользователем (существуют регулируемые
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.