Оптика
Все действия света характеризуются вектором напряжённости.
Уравнение
электромагнитной волны: 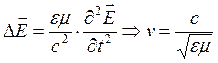 . В прозрачных средах
. В прозрачных средах 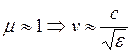 . Показатель преломления среды
. Показатель преломления среды 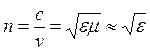 . Т.к. e
зависит от частоты колебаний, то
. Т.к. e
зависит от частоты колебаний, то ![]() .
.
Волновая поверхность – геометрическое место точек, колеблющихся в одинаковой фазе.
Длина волны в
среде 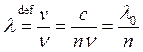 , где
, где ![]() – длина
волны в вакууме.
– длина
волны в вакууме.
Модуль среднего
по времени значения плотности потока энергии, переносимой волной, называется
интенсивностью волны: ![]() . Т.к.
. Т.к. ![]() , то
, то 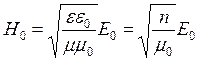 .
Пусть
.
Пусть ![]() . Тогда
. Тогда 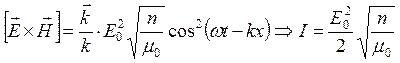 .
.
Свет излучается
цугами. Каждый цуг длится порядка ![]() с.
с.
В однородной среде свет распространяется прямолинейно (при отсутствии маленьких отверстий). При пересечении световых лучей они не возмущают друг друга (при не слишком больших интенсивностях).
Отражённый луч лежит в одной плоскости с падающим и с перпендикуляром, восстановленным в точке падения, причём угол падения равен углу отражения.
Закон преломления: 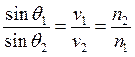 , где
, где ![]() – угол
преломления,
– угол
преломления, ![]() – скорость в i-й
среде,
– скорость в i-й
среде, ![]() – преломление i-й
среды.
– преломление i-й
среды.
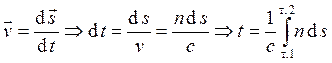 .
.
Оптическая длина пути 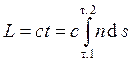 .
.
Принцип Ферма: Свет распространяется по такому пути, оптическая длина которого минимальна.

![]()
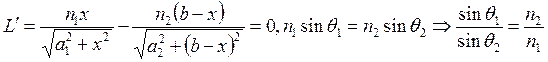 .
.
Интерференция световых волн
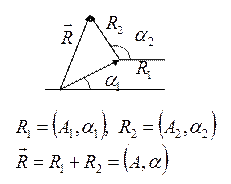 Пусть в какую-то
точку приходят две волны:
Пусть в какую-то
точку приходят две волны: ![]() ,
, ![]() . Тогда амплитуда результирующего колебания
. Тогда амплитуда результирующего колебания
![]() . Усреднив по времени, получим:
. Усреднив по времени, получим: ![]() (где
(где ![]() ),
следовательно,
),
следовательно, ![]() .
.
Если разность
фаз d остаётся постоянной по
времени, то такие лучи называются когерентными. Тогда ![]() .
.
Явление перераспределения интенсивности называется интерференцией.
Пусть один луч
расщепили на два и пустили их по путям ![]() и
и ![]() . Тогда у начального луча фаза
. Тогда у начального луча фаза ![]() , у расщеплённых –
, у расщеплённых – 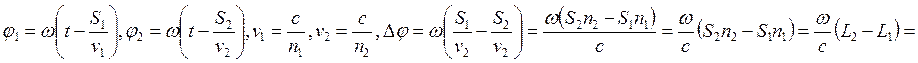
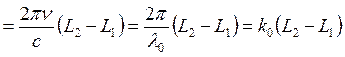 . Когда оптическая разность хода
. Когда оптическая разность хода ![]() , будет максимум распределения
интенсивности, а когда
, будет максимум распределения
интенсивности, а когда 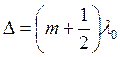 , будет минимум
распределения интенсивности.
, будет минимум
распределения интенсивности.
Интерференция от двух источников
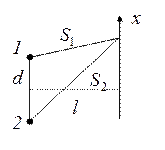
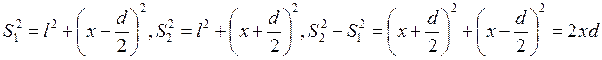 – разность хода. При этом
– разность хода. При этом 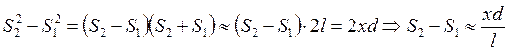 . Оптическая разность хода
. Оптическая разность хода 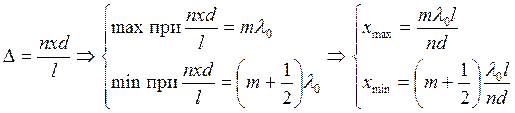 , где m –
любое целое число. Отсюда видно, что ширина интерференционной полосы
, где m –
любое целое число. Отсюда видно, что ширина интерференционной полосы 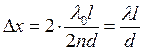 .
.
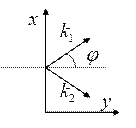 Пусть
распространяются две волны:
Пусть
распространяются две волны: ![]() ,
, ![]() . Суммарная волна
. Суммарная волна ![]()
![]() . Отсюда видно, что амплитуда суммарного
колебания
. Отсюда видно, что амплитуда суммарного
колебания ![]() зависит от точки экрана, в которую она
попадает. Если
зависит от точки экрана, в которую она
попадает. Если ![]() , то наблюдается максимум,
следовательно,
, то наблюдается максимум,
следовательно, 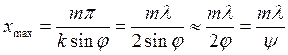 , где y – угол между волнами.
, где y – угол между волнами.
Интерференция на тонких пластинах
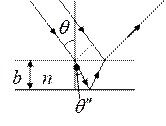 Оптический путь
левого луча внутри пластинки:
Оптический путь
левого луча внутри пластинки: 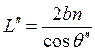 . Оптический путь
правого луча, проходимый им в то время, пока второй луч идёт внутри пластинки:
. Оптический путь
правого луча, проходимый им в то время, пока второй луч идёт внутри пластинки: ![]() . Оптическая разность хода:
. Оптическая разность хода: 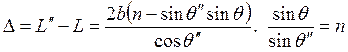 , следовательно,
, следовательно, 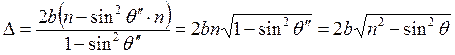 .
.
При отражении от границы раздела двух сред, если вторая среда более оптически плотная, то происходит скачок фазы на p.
Следовательно, 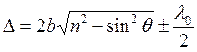 .
.
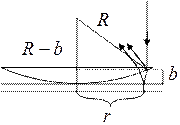 Найдём
Найдём 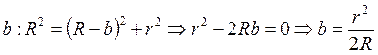 , следовательно, оптическая разность хода
, следовательно, оптическая разность хода 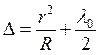 . Если
. Если ![]() , то
кольцо светлое. Если
, то
кольцо светлое. Если 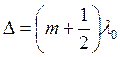 , то кольцо тёмное.
, то кольцо тёмное.
Радиус m-го кольца: 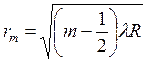 .
.
Временная когерентность
Пусть есть цуг,
растянутый во временном промежутке 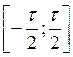 с амплитудой
с амплитудой ![]() при
при 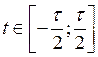 .
Разложим его в интеграл Фурье:
.
Разложим его в интеграл Фурье: 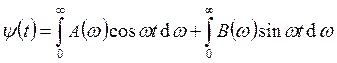 , где
, где 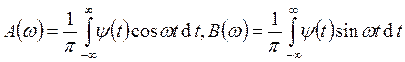 . При этом
. При этом ![]() , т.к.
, т.к. ![]() – нечётная функция, а
– нечётная функция, а 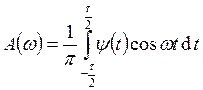 , т.к.
, т.к. ![]() при
при 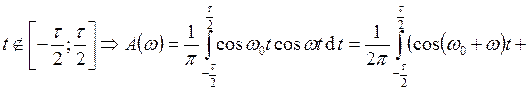
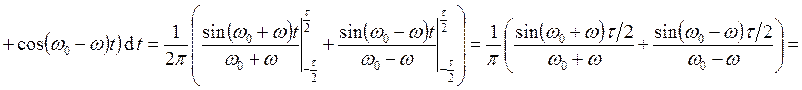
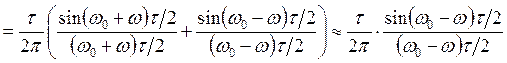 , т.к. w
и
, т.к. w
и ![]() – большие частоты.
– большие частоты.
Интенсивность
света 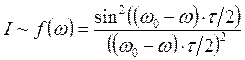 .
.
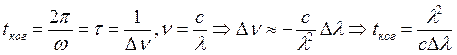 .
.
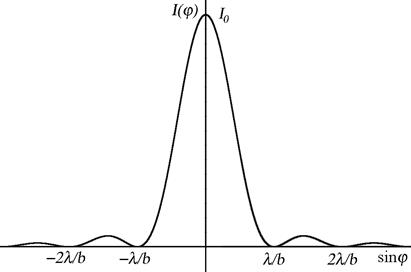 Время
когерентности – это то время, за которое случайное изменение фазы колебания
достигнет значения порядка p.
Время
когерентности – это то время, за которое случайное изменение фазы колебания
достигнет значения порядка p.
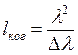 – длина когерентности – то расстояние,
которое волна проходит за время когерентности.
– длина когерентности – то расстояние,
которое волна проходит за время когерентности.
Если оптическая
разность хода порядка ![]() , то эти два луча становятся
некогерентными.
, то эти два луча становятся
некогерентными.
Вернёмся к
пластинке: 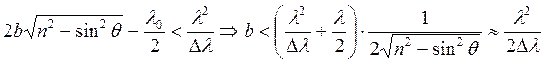 , т.к.
, т.к. ![]() .
.
Таким образом,
толщина b должна быть порядка ![]() м.
м.
Пространственная когерентность
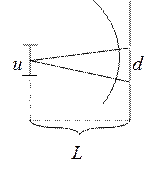 Пусть в
пространстве распространяется сферическая волна. Выясним, какое максимальное
расстояние d между двумя точками на её фронте
можно взять, при котором волна всё ещё будет когерентна сама себе. Для этого
можно обернуть картину и представить, что свет, излученный двумя точечными
источниками, находящимися на расстоянии d
попадает в точку с координатой u. Тогда
оптическая разность хода
Пусть в
пространстве распространяется сферическая волна. Выясним, какое максимальное
расстояние d между двумя точками на её фронте
можно взять, при котором волна всё ещё будет когерентна сама себе. Для этого
можно обернуть картину и представить, что свет, излученный двумя точечными
источниками, находящимися на расстоянии d
попадает в точку с координатой u. Тогда
оптическая разность хода 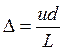 и если
и если 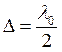 , то волны будут когерентны.
, то волны будут когерентны. 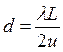 – ширина когерентности – предельное
расстояние на фронте волны, в двух точках которого волны ещё когерентны. Угол
когерентности
– ширина когерентности – предельное
расстояние на фронте волны, в двух точках которого волны ещё когерентны. Угол
когерентности 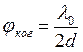 .
.
Дифракция
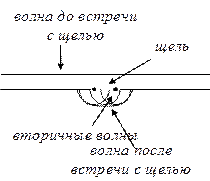 Принцип
Гюйгенса: Каждая точка волнового фронта является источником вторичных волн,
а огибающая этих вторичных волн есть новое положение фронта волны.
Принцип
Гюйгенса: Каждая точка волнового фронта является источником вторичных волн,
а огибающая этих вторичных волн есть новое положение фронта волны.
Принцип Гюйгенса-Френеля: Амплитуда вторичной волны пропорциональна площади элемента, который её испускает.
Уравнение
волны, испущенной площадкой 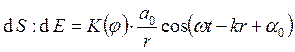 , где j – угол между нормалью к площадке и
направлением, в котором рассматривается излучение,
, где j – угол между нормалью к площадке и
направлением, в котором рассматривается излучение, ![]() –
коэффициент, введённый Френелем,
–
коэффициент, введённый Френелем, 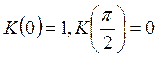 ,
, ![]() – фаза колебания в точке на поверхности
фронта. Уравнение всего волнового фронта:
– фаза колебания в точке на поверхности
фронта. Уравнение всего волнового фронта: 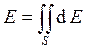 , где S – его площадь (например, на рисунке это площадь щели).
, где S – его площадь (например, на рисунке это площадь щели).
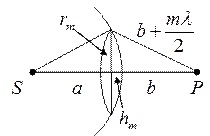
Зоны Френеля
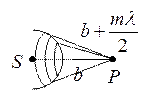 Зоны, ограниченные
точками с расстоянием от волнового фронта до точки P,
равном
Зоны, ограниченные
точками с расстоянием от волнового фронта до точки P,
равном 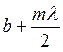 , называются зонами Френеля.
, называются зонами Френеля.
Разность фаз у соответствующих волн из разных зон Френеля равна p.
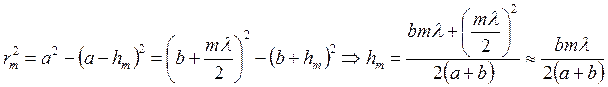
 .
.
Площадь
сегмента 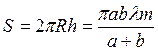 . Площадь зоны
. Площадь зоны 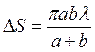 .
.
 Если углы очень
малы, то
Если углы очень
малы, то ![]() . Тогда амплитуда колебаний в точке P
. Тогда амплитуда колебаний в точке P ![]() , где
, где ![]() – амплитуда колебания, приходящего из i-й зоны Френеля;
– амплитуда колебания, приходящего из i-й зоны Френеля; 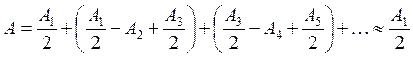 , т.к.
, т.к.
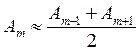 .
.
Радиус m-й зоны 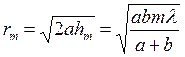 .
.
Количество зон,
открываемых отверстием радиуса 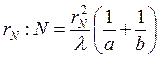 .
.
Дифракция Фраунгофера
 Так как, согласно
принципу Гюйгенса-Френеля, амплитуда пропорциональна площади излучающей
поверхности, а она в случае, изображённом на рисунке, пропорциональна ширине
отрезка, лежащего в щели, то
Так как, согласно
принципу Гюйгенса-Френеля, амплитуда пропорциональна площади излучающей
поверхности, а она в случае, изображённом на рисунке, пропорциональна ширине
отрезка, лежащего в щели, то ![]() . Амплитуда приходящей
волны
. Амплитуда приходящей
волны 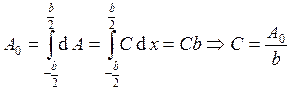 .
.
Разность хода ![]() ; сдвиг фазы
; сдвиг фазы 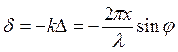 .
.
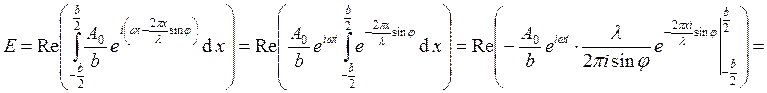
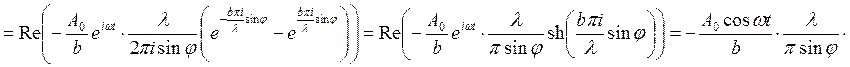
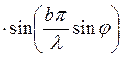 . Интенсивность
. Интенсивность 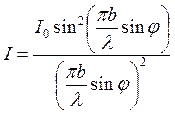 .
Количество минимумов
.
Количество минимумов 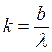 (т.к.
(т.к. ![]() ).
Угловая ширина центрального максимума
).
Угловая ширина центрального максимума 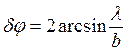 .
.
Количественный критерий дифракции Френеля и дифракции Фраунгофера
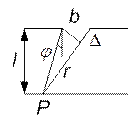
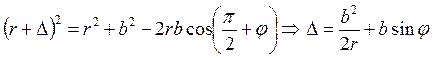 . Если лучи параллельны, то
. Если лучи параллельны, то ![]() .
. 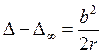 . Если
. Если
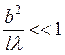 , то наблюдается дифракция Фраунгофера
(т.к. порядок l примерно такой же, как и у r), если
, то наблюдается дифракция Фраунгофера
(т.к. порядок l примерно такой же, как и у r), если 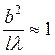 , то наблюдается
дифракция Френеля, а если
, то наблюдается
дифракция Френеля, а если 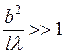 , то
, то 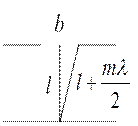 дифракции
дифракции
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.