Изучение колебаний связанных маятников. Определение частот нормальных и парциальных колебаний системы из двух одинаковых маятников

Обнинский  Государственный Технический Университет Атомной Энергетики.

ФИЗИКО-ЭНЕРГЕТИЧЕСКИЙ ФАКУЛЬТЕТ.

Кафедра  общей    и   специальной  физики.

Лабораторная работа № 5.

Тема:

«Изучение колебаний связанных маятников».

Выполнил: Евстигнеев Е. Ю.

Проверил:  Вишератин К. Н.

Обнинск 2003

Теория.

Два математических маятника, связанные между собой пружиной, являются простейшим примером связанной системы.

Как известно, для математического маятника уравнение моментов имеет вид

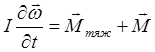                                                                                       (1)

где  - момент силы тяжести; - моменты остальных сил.

В случае связанных маятников на каждый из них будет действовать со стороны пружины дополнительная сила , которая при небольших отклонениях может быть рассчитана как

,                                                                   (2)

где l₁- расстояние от точки подвеса до точки закрепления пружины,

k- коэффициент жёсткости пружины,

 и - углы отклонения первого и второго маятников соответственно.

Эта сила создаёт дополнительный момент . Ограничиваясь рассмотрением простейшего случая, когда оба маятника имеют одинаковую длину l, а точки закрепления пружин находятся на одинаковом расстоянии l₁ от оси подвеса, из (1) в проекции на ось, перпендикулярную плоскости чертежа, получим для первого и второго маятников соответственно

                                                              (3)

                                                                     (4)

где учтено что ; I=; .

Преобразовав (3) и (4), получаем

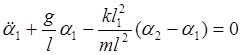                                                                       (5)

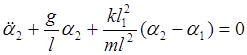                                                                       (6)

Обозначим , .

Складывая и вычитая (5) и (6), получим

                                                                                               (7)

                                                                                              (8)

где 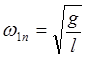                 - первая нормальная частота;                 (9)

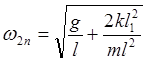- вторая нормальная частота.     (10)

Решения уравнений (7) и (8) имеют вид

                                                                                   (11)

                                                                    (12)

Для углов отклонения получаем

                                                (13)

                                                 (14)

Выполнение работы.

Упражнение №1. Определение частот нормальных и парциальных колебаний системы из двух одинаковых маятников.

1. Устанавливаю обоймы, крепящие пружины, в верхней части стержней маятников, а грузы – в нижней части (для обоих маятников на одинаковом расстоянии)

2. Отсоединяю систему от обоймы, соединяющей маятник со стержнем электромотора.

3. Нажимаю кнопку СЕТЬ.

4. Отклоняю маятники сначала в одну (), затем в противоположные () стороны на угол ~ 6˚ и отпускаю их.

5. Провожу замеры времени 10 периодов колебаний. Данные записываю в Табл. №1.

Так же в таблицу №1 вношу  некоторые рассчитанные величины (t_{1п ср}, t_{2п ср}, t_1п, t_2п, , , k,  где )

Таблица №1.

Длинна, см	№	Время		t1п ср	t2п ср	t1п	t2п			k
		t1п	t2п
l1= 10	1	12,079	12,044					5.2	5.224
	2	12,089	12,021
	3	12,072	12,011
	4	12,078	12,032
	5	12,072	12,038
l2= 15	1	12,035	11,671					5.22	5.382
	2	12,034	11,673
	3	12,039	11,676
	4	12,036	11,674
	5	12,037	11,675
l3=20	1	12,032	9,471					5.224	6.636
	2	12,026	9,465
	3	12,027	9,467
	4	12,028	9,470
	5	12,030	9,468
l4=25	1	12,053	6,800					5.21	9.243
	2	12,056	6,791
	3	12,058	6,798
	4	12,054	6,803
	5	12,057	6,801
l5=30	1	12,085	4,545					5.2	13.737
	2	12,079	4,551
	3	12,080	4,532
	4	12,083	4,533
	5	12,084	4,561

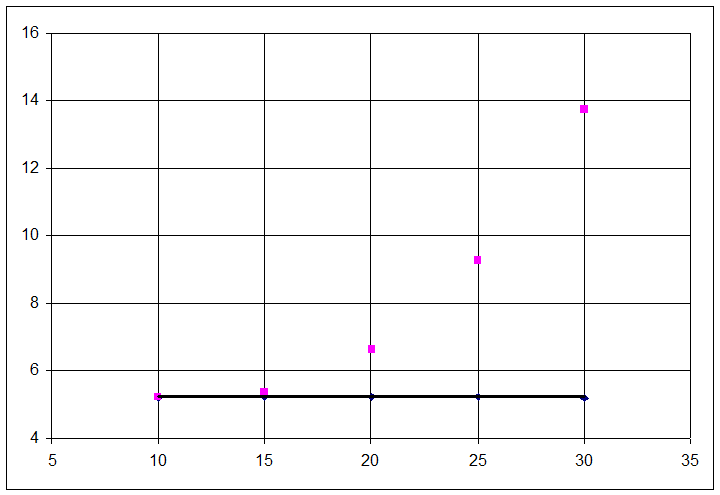
6. Строю график зависимостей (l₁), (l₁).

Упражнение №2. Изучение резонанса в системе связанных маятников.

Изменяя обороты двигателя и выжидая установления колебаний, провожу измерение амплитуды колебаний второго маятника по шкале.

Данные заношу в таблицу №2.

Таблица №2.

Частоты двигателя, причём 1<2<3
1	2	3
t1	t2	t3
13.147	11.067	10.688
13.137	11.070	10.685
13.141	11.074	10.689
13.144	11.078	10.686
13.139	11.080	10.687
tср
13,141	11,074	10,687
t			1п	2п	3п
0,657	4,78	5,674	4,78	5,674	5,88

При дальнейшем увеличении оборотов двигателя наблюдал резкое увеличение амплитуды колебаний и их частоты. Данное явление называется резонансом.