Определение скорости пули с помощью баллистического крутильного маятника

Работа №9

Определение скорости пули с помощью баллистического крутильного маятника.

группа ………

выполнил…………………………..

проверил ……….…………………

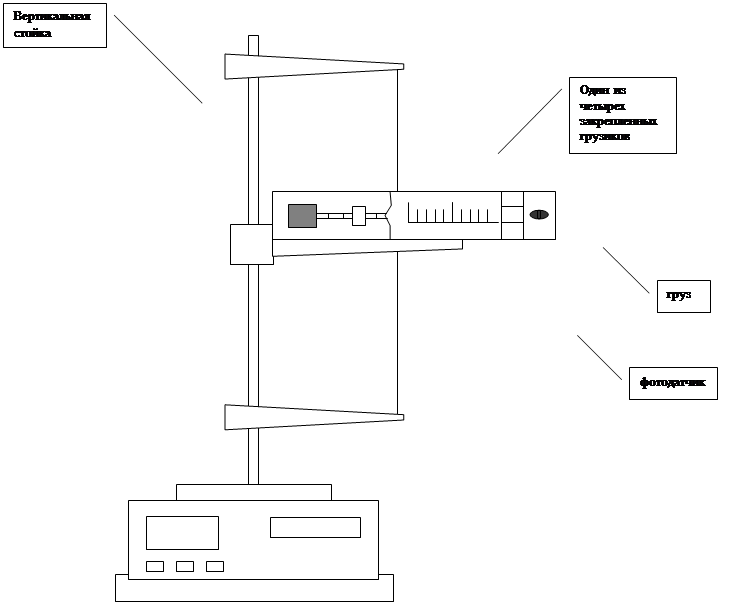
Общий вид установки (баллистического крутильного маятника).

 

№ измерения	t0, c	t1, c (m1)	t2, c (m2)
1	6,124	4,329	3,540
2	6,136	4,320	3,531
3	6,118	4,311	3,536
<ti>	6,126	4,32	3,536

<t>=(1/n)∙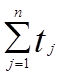 - вычисление среднего арифметического.

<t₀>=6,126

<t₁>=4,32

<t₂>=3,536

S_n=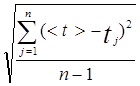 - вычисление средней квадратичной погрешности.

S_n(t₀)=                                     S_n(t₁)=                                   S_n(t₂)=     

S=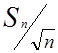 - вычисление средней квадратичной погрешности среднего арифметического.

S(t₀)=                                       S(t₂)=                                     S(t₁)=

∆t_cл=t_α,n∙S - вычисление случайной погрешности; α=0,95; n=3, значит из таблицы коэффициентов Стьюдента следует, что t_α,n=4,3

∆t= - абсолютная погрешность; ∆t_сист (2∙10^-4 c)– систематическая погрешность.    

∆t₀=                                          ∆t₁=                                          ∆t₂=

δ=∆t/<t> - относительная погрешность.

δ(t₀) =                                        δ(t₁) =                                       δ(t₂) =      

Момент инерции маятника.

I_c1=m∙r∙((gt²/2S)-1)      (r-радиус валика, m-масса маятника)

(m_а=m₁+ m_д+ m_в ;  m_b=m₂+ m_д+ m_в)

<I_c1a>=m_a∙r∙((g<t_a>²/2S)-1)=

<I_c1b>=m_b∙r∙((g<t_b>²/2S)-1)=

δI_c1=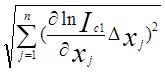 - относительная погрешность

(n=3 , x₁=r , x₂=t , x₃=S)

δI_c1= 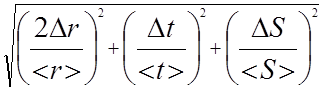     ,  (∆r=5∙10^-4 м ; ∆S=5∙10^-4 м)

δI_c1a=

δI_c1b=

∆ I_c1= δI_c1∙< I_c1>   - абсолютная погрешность

∆I_c1a=                                                            ∆I_c1b=

I_c1=< I_c1>±∆ I_c1

I_c1a=                                                                 I_c1b=

(δI_c1a=                        δI_c1b=                           α=0,95)

Момент инерции маятника.

I_c2=I_в+I_д+I_к       (I_в- момент инерции валика, I_д- момент инерции диска, I_к –момент инерции кольца.)

I_в=(1/2)m_вr²  ,   I_д=(1/2)m_д(R²+r²)   ,   I_к=(1/2)m_к(R+R₁)         (R₁-внешний радиус кольца, R-внутренний радиус кольца, m_д=(102,0±0,1)г, m_в=(31,0±0,1)г)

< I_c2> = I_в+I_д+I_к=

<I_c1a> =

<I_c1b> =

∆ I_c1= 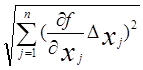    -    абсолютная погрешность     (x₁=r; x₂=R; x₃=R₁; n=3)

∆ I_c1=

∆ I_c1a=                                                   ∆ I_c1b=

δI_c2=∆ I_c2/<I_c2>  - относительная погрешность

δI_c2a=

δI_c2b=

I_c2= <I_c2> ± ∆ I_c2   ;     I_c2a=                                            I_c2b=

(δI_c2a=                           δI_c2b=                            α=0,95)

Вывод: