
Задача №19
Берем ур-ие Максвелла 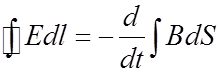 .
Здесь под интегралами везде векторы. Справа стоит производная от потока вектора
B.
.
Здесь под интегралами везде векторы. Справа стоит производная от потока вектора
B.
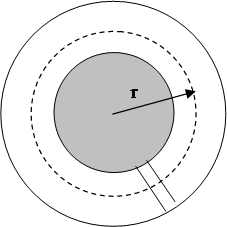
На рисунке показан вид с торца.
Для нашего случая выбираем в качестве контура интегрирования для левого интеграла силовую линию вихревого электрического поля, показанную на рисунке пунктиром. Напряженность поля будем подставлять в виде D/ee0. На силовой линии напряженность совпадает по направлению с элементом дуги dl, и потому cos угла между ними равен 1, и скалярное произведение E на dl сводится к умножению модулей векторов. На силовой линии E постоянно и потому может быть вынесено из-под интеграла. Тогда получим
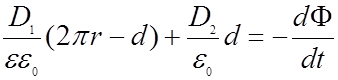 , где D1 относится к
диэлектрику, а D2 – к воздушному
зазору, шириной d. Нормальная составляющая
вектора D не изменяется на границе раздела двух
диэлектриков, и потому D1=D2.
, где D1 относится к
диэлектрику, а D2 – к воздушному
зазору, шириной d. Нормальная составляющая
вектора D не изменяется на границе раздела двух
диэлектриков, и потому D1=D2.
Следовательно:
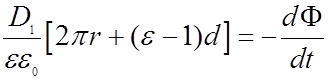
Значит
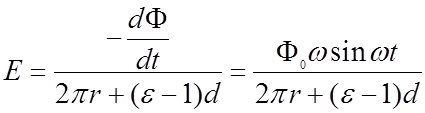 .
.
Ширина зазора в задаче не дана. По-видимому, предполагается, что ею можно пренебречь.
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.