Теоретические вопросы и практические задания на контрольную работу по курсу "Теория принятия решений" (Роли людей в процессе ПР. Понятие рационального выбора. Идеальный/неидеальный эксперимент)

1. Когда имеет смысл для уточнения условий в данной неопределенной ситуации предпринять некоторый эксперимент?
2. Как вычислить допустимую стоимость эксперимента?
3. Как оценить целесообразность эксперимента?
4. Дать определение теоремы Байеса.
5. В чем состоит идеальный эксперимент?
6. Что называют неидеальным экспериментом?

Вариант 1

1. Матрица решений.

2.  Выбрать оптимальную альтернативу.  Определить целесообразность эксперимента, стоимость которого равна 1.

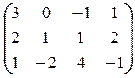,       Pj={0.3,0.1,0.4,0.2}

3. Альтернативы заданы оценками по 3-м критериям: f₁® max, f₂®max, f₃®min, х₁(3,2,2), х₂(6,1,5), х₃(3,6,4), х₄(4,0,7), х₅(5,4,6), х₆(4,2,3), х₇(2,5,6), х₈(1,3,5).

Вариант 2

1. Роль и значение вектора результатов.

2.  Выбрать оптимальную альтернативу

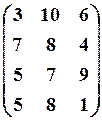
3. Альтернативы заданы оценками по 3-м критериям: f₁® min, f₂®max,  f₃® max, c₁:c₂:c₃=1:2:4:

х₁(5,1,6), х₂(6,7,3), х₃(3,4,4), х₄(1,2,6), х₅(4,2,7), х₆(2,6,4), х₇(5,8,3).

Вариант 3

1. Природные неопределенности.

2. Выбрать оптимальную альтернативу.

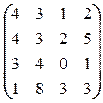,       Pj={0.1,0.4,0.4,0.1}

3. Альтернативы заданы оценками по 2-м критериям: f₁® min, f₂®max, х₁(2,8), х₂(1,5), х₃(5,7), х₄(4,9), х₅(5,4), х₆(4,5), х₇(2,7), х₈(5,9).

Вариант 4

1. Типы неопределенности в задачах принятия решений.

2.  Выбрать оптимальную альтернативу. Оценить, целесообразен ли эксперимент, стоимость которого равна 0,5.

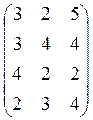 ,       Pj={0.1,0.5, 0.4}.

3. Альтернативы заданы оценками по 3-м критериям: f₁® max, f₂®max, f₃®min, f₁³f_2,  f₂ ² f₃.

х₁(3,1,2), х₂(6,7,1), х₃(3,6,4), х₄(1,10,2), х₅(5,4,6), х₆(0,2,3), х₇(2,5,8), х₈(1,9,5).

Вариант 5

1. Алгоритм решения многокритериальных задач.

2.  Выбрать оптимальную альтернативу

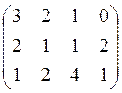,       Pj={0.2,0.3,0.4,0.1}

3. Альтернативы заданы оценками по 3-м критериям: f₁® max, f₂®max, f₃®max

х₁(3,2,5), х₂(6,7,1), х₃(3,6,3), х₄(3,10,2), х₅(5,4,6), х₆(4,2,3), х₇(2,5,3), х₈(3,9,2).

Вариант 6

1. Множество Парето.

2.  Выбрать оптимальную альтернативу

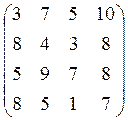
3. Альтернативы заданы оценками по 2-м критериям: f₁® min, f₂®max, c₁:c₂=3:2

х₁(1,6), х₂(7,2), х₃(6,3), х₄(2,9), х₅(3,4), х₆(6,2), х₇(8,5), х₈(5,8).

Вариант 7

1. Решение МКЗ с помощью свертки

2. Выбрать оптимальную альтернативу

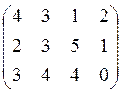 ,       Pj={0.2,0.1,0.4,0.3}.

3. Альтернативы заданы оценками по 4-м критериям: f₁® max, f₂®max,  f₃® min, f₄® min:

х₁(8,3,4,1), х₂(7,5,3,2), х₃(6,3,1,2), х₄(8,2,3,1), х₅(4,6,2,7), х₆(2,3,0,2), х₇(5,8,6,3).

Вариант 8

1.  Методы решения МКЗ при равнозначных критериях.

2. Выбрать оптимальную альтернативу. Возможен ли эксперимент, стоимость которого равна 1?

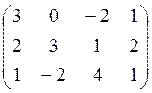,       Pj={0.3,0.3,0.1,0.3}

3. Альтернативы заданы оценками по 3-м критериям: f₁® min, f₂®max, f₃®max, c₁:c₂:c₃=5:2:1, х₁(3,5,9), х₂(5,7,3), х₃(3,6,5), х₄(1,10,3), х₅(5,5,7), х₆(0,7,3), х₇(2,9,5), х₈(1,7,8).

Вариант 9

1. Принцип Парето

2. Выбрать оптимальную альтернативу.

      

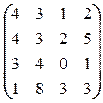
3. Альтернативы заданы оценками по 2-м критериям: f₁® max, f₂®max, х₁(3,8), х₂(4,7), х₃(3,7), х₄(1,10), х₅(5,9), х₆(4,6), х₇(5,6), х₈(8,7).

Вариант 10

1. Однородная шкала оценок

2. Выбрать оптимальную альтернативу

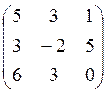
3. Альтернативы заданы оценками по 4-м критериям: f₁® max, f₂®max, f₃®min, f₄®min: c₁:c₂:c₃:c₄=1:2:3:4;

х₁(5,1,2,2), х₂(6,3,1,3), х₃(3,5,4,1), х₄(2,1,6,5), х₅(5,7,6,4), х₆(7,2,3,1), х₇(4,5,3,3), х₈(6,9,5,4).

 

Вариант 11

1.  Минимаксный критерий

2. Выбрать оптимальную альтернативу.

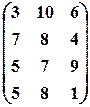 Pj={0.1,0.5, 0.4}.

3. Альтернативы заданы оценками по 3-м критериям: f₁® min, f₂®max,  f₃® max:

х₁(2,8,6), х₂(3,7,5), х₃(4,6,8), х₄(1,6,7), х₅(4,8,7), х₆(2,5,6), х₇(5,8,8).

Вариант 12

1. Критерий Байеса-Лапласа

2. Выбрать оптимальную альтернативу. Оценить, целесообразен ли эксперимент, стоимость которого равна 3.

 ,       Pj={0.1,0.5, 0.4}.

3. Альтернативы заданы оценками по 3-м критериям: f₁® max, f₂®max, f₃®min:

х₁(3,7,2), х₂(4,7,3), х₃(3,6,4), х₄(6,10,2), х₅(5,6,4), х₆(10,2,3), х₇(5,5,8), х₈(5,9,2).

Вариант 13

1. Критерий Сэвиджа

2.  Выбрать оптимальную альтернативу

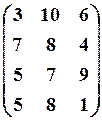
3. Альтернативы заданы оценками по 3-м критериям: f₁® min, f₂®max,  f₃® max, c₁:c₂:c₃=1:5:4:

х₁(3,1,6), х₂(4,7,3), х₃(3,4,4), х₄(1,5,6), х₅(4,6,7), х₆(1,6,4), х₇(5,6,3).

Вариант 14

1. Критерий Гурвица

2. Выбрать оптимальную альтернативу.

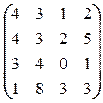,       Pj={0.1,0.4,0.4,0.1}

3. Альтернативы заданы оценками по 2-м критериям: f₁® min, f₂®max, х₁(2,8), х₂(3,5), х₃(5,7), х₄(4,9), х₅(6,4), х₆(1,7), х₇(2,6), х₈(5,8).

Вариант 15

1. Критерий линейной свертки

2.  Выбрать оптимальную альтернативу. Оценить, целесообразен ли эксперимент, стоимость которого равна 0,5.

 ,       Pj={0.1,0.6, 0.3}.

3. Альтернативы заданы оценками по 3-м критериям: f₁® max, f₂®max, f₃®min, f₁²f_2,  f₂ ³ f₃.

х₁(3,4,2), х₂(6,7,3), х₃(4,6,3), х₄(4,10,2), х₅(4,5,3), х₆(1,5,3), х₇(2,5,8), х₈(6,4,5).

Вариант 16

1. Алгоритм решения многокритериальных задач.

2.  Выбрать оптимальную альтернативу

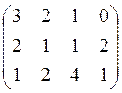,       Pj={0.2,0.3,0.4,0.1}

3. Альтернативы заданы оценками по 3-м критериям: