








происходит в результате эксперимента, то есть единственное событие, включающее все без исключения элементарные исходы — событие Ω.
2.Невозможным называется событие, которое не может произойти в результате эксперимента, то есть событие, не содержащее ни одного элементарного исхода
(пустое множество ![]() ). Заметим, что всегда
). Заметим, что всегда ![]()
![]() Ω.
Ω.
С событиями м работать как с обычными мн-вами.
![]() - А не
произошло
- А не
произошло
А+В=АÈВ сумма событий. Это событие состоящее в том, что произошло или А, или В, или оба вместе.
АВ=АÇВ произошло и А и В одновременно
Если АВ=Æ то А и В – несовместимые события:
А\В разность событий (произошло А и не произошло В)
![]()
Св-ва событий:
![]()
Для решения задач ТВ необходимо иметь специальный класс мн-в, называемый алгеброй событий.
Опр. L - алгебра событий, if:
1. WÎL;
2. if А ÎL, то Ā ÎL;
3. if А и В ÎL, то А+В ÎL, АВ ÎL. 1-3 аксиомы алгебры
Опр. Алгебра L наз. s - алгеброй, if для любой ¥ посл-ти событий {Аn}, АnÎL"n выполняется SAnÎL,PAnÎL
5 Вероятностная мера. Теорема об эквивалентности систем аксиом
Аксиомы вероятности:
Р1: Р(W)=1 (акс. нормировки)
Р2: " А Î L, Р(А) ³0 (не отрицательности)
Р3: А,В Î L, АВ=Æ, то Р(А+В)=Р(А)+Р(В) (аддетивность)
Р4: Аn¯Æ limP(A)=0 (непрерывность)
P3*:Если В1…Bn последовательность попарно несовместные события BiBj=0,i<>j то
![]() Th об
эквивалентности аксиом P1…P4ßà P1…P3*
Th об
эквивалентности аксиом P1…P4ßà P1…P3*
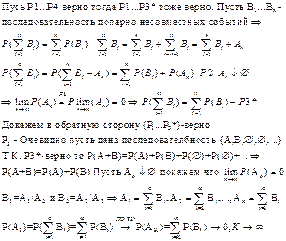
8 Дискретное ПЭИ. Пример.
Предположим, что мы имеем дело с дискретным пространством элементарных исходов, то есть пространством, состоящим из конечного или счетного числа элементов:
Ω = {ω1,ω2,... ,ωn,...}.
Определение 6. Поставим каждому элементарному исходу
ωiÎ Ω в соответствие число p(ωi) ∈ [0,1] так, что
![]()
Назовем число p(ωi) вероятностью элементарного исхода ωi. Вероятностью события A ∈Ω называется число
![]() равное сумме вероятностей элементарных исходов, входящих
в множество А.
равное сумме вероятностей элементарных исходов, входящих
в множество А.
Предположим, что мы имеем дело с пространством элементарных исходов, состоящим из конечного числа N элементов: Ω = {ω1,ω2,... ,ωn}.- Более того, предположим, что из каких-либо соображений мы можем считать элементарные исходы равновозможными. Тогда вероятность любого из них принимается равной 1/N.
Если событие А = {ω1,ω2,... ,ωk} состоит из к элементарных исходов, то вероятность этого события равняется отношению k/N:
Р(А) = p(ω1,)+…+p(ωk) ,=k•1/N=|A|/|Ω | где символом |А| обозначено число элементов конечного множества А.
2 Игрока поочерёдно бросают монету выигрывает тот у кого первого выпадает «ОРЁЛ»
Ω={o,po,ppo,pppo,….}= {ω1,ω2,... }
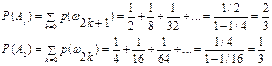
3 Предел последовательности событий
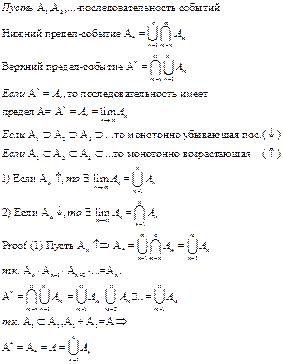
6 Вероятностная мера. Теорема сложения. Задача о фуражках
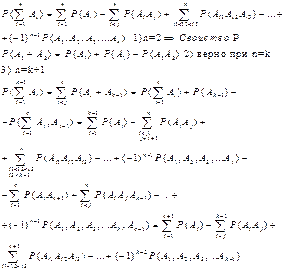 Задача
о фуражках
Задача
о фуражках
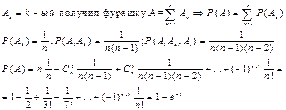
9 Геометрические вероятности. Задача Бюффона.
применяется в том случае, когда классической схемой пользоваться нельзя: |W|=¥.
P(A)=m(A)/m(W) В качестве меры m мб длина, объем, площадь…
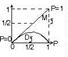
Задача Бюффона: На пл-ть, расчерченную êê прямыми, расстояние му к-ыми d, наугад брошена игла. Найти вер-ть того, что игла пересечет какую-нить из прямых.
Дано: lиглы=l; d (l<d)
![]() х – расстояние от центра иглы, до ближайшей
прямой; j - угол му иглой и прямой. х Î [0;d/2];
х – расстояние от центра иглы, до ближайшей
прямой; j - угол му иглой и прямой. х Î [0;d/2];
j Î [0;p]
W: {(х, j) ç х Î [0;d/2]; j Î [0;p]}; Проекция половинки иглы на вертикаль =sinj×l/2.
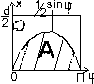 if х > sinj×l/2
то пересечения не будет;
if х > sinj×l/2
то пересечения не будет;
if x £ sinj×l/2 то пересечение произойдет.
А= {игла пересечет прямую}={(х, j)çх £ sinj×l/2};
![]()
Эксперименты состояли в оценивании числа π:
P(A)= ![]() ; nn/n®P(A) π »
; nn/n®P(A) π »![]() ; π » 3,21; π » 3,165…
; π » 3,21; π » 3,165…
Чем > число испытаний, тем более точное получается π. Этот эксперимент по сути явл. методом Монте-Карло (статистических испытаний). Ограничение на использование геометрической схемы: Случайная точка д.б. равномерно распределена на W.
10 Условная вероятность. Задача о письменном столе
Определение Условной вероятностью события А, при условии, что произошло событие В, называется число
РВ(А)=P(AB)/P(B)=Р(А çB );
Будем считать, что условная вероятность определена только в случае, когда Р(В) > 0.
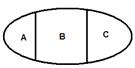
Задача о письменном столе
В столе 8 ящиков находится письмо, вероятность что оно в одном из 8 =0.1 Открыли 5 ящиков и письма нет. Найти вероятность того что в 3 остальных оно есть
B=писмо в остальных 3 ящтках
А=письмо в первых пяти
С=в столе нет письма.
13 Формула Байеса. Пример
Формула Байеса позволяет переоценить вероятность гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.
Вероятность появления события А пред. Формулой
Пусть события H1,H2,…,Hn образуют коечное разбиение
![]()
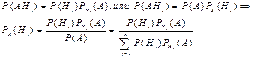
ф-ла Байеса.
Ех. 3 машины, I изготовляет – 25%, II – 35%, III – 40%. Брак в их продукции составляет 5%, 4%, 2% соответственно. Найти вер-ть событий: а). случайно выбранное изделие браковано; б). случайно выбранной изделие прозведено на I машине, при условии, что оно браковано.
Решение:
А={изделие брак.}; Вi={изделие произведено i-машиной}
![]() -
конечное разбиение. ВiBj=Æ if i¹j SBi=W => B1,B2,B3 – конечное разбиение.
-
конечное разбиение. ВiBj=Æ if i¹j SBi=W => B1,B2,B3 – конечное разбиение.
Дано: Р(В1)=25/100; P(B2)=35/100; P(B3)=40/100; P(A/B1)=5/100; P(A/B2)=4/100; P(A/B3)=2/100 а) Р(А); б) P(B1/A); P(B2/A); P(B3/A)- ?
P(A)=P(B1)P(A/B1)+ P(B2)P(A/B2)+ P(B3)P(A/B3)=3,45% - такова вер-ть брака
P(B1/A)=125/345; P(B2/A)=140/345; P(B3/A)=80/345
16 Полиномиальная схема
Задача Генерируется случ. образом послед. чисел 012345 длины n наити вероятность того что в выбраной последовательности будет M1-“0”,M2-1 или 2 M3-3,4, или 5.
1) Классический вариант решения.
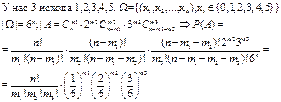
Если возможно S
исходов (S>2), и даны вероятности Pi(i=1,2,..S) и
даны вероятности каждого исхода то P(M1-Раз 1-й
исход,M2-раз 2-й исход,…,Ms-раз-s-й
исход)говорят о полиномиальной схеме. ![]()
Пример:
Выбирается n шаров с ВОЗВРАЩЕНИЕМ б-2,з-3,к-5.
![]()
11 Независимость событий. Теорема умножения.
Опр. События А и В независимы, если и только если Р(АВ)=Р(А)Р(В).
Критерий независимости
Событие А не зависит от события В, if РВ (А)=Р(А) , т.е.
P(A/B)=P(A) или Р(АВ)=Р(А)Р(В)
P(AB)=PB(A)P(B).
Th умножения:
Независимость событ. Ех Бернштейна
Рассмотрим посл-ть событий А1, А2, …, Аn
Опр. Говорят, что эта посл-ть обладает попарной независимостью, if Р(АiАj)=Р(Аi)Р(Аj) " i¹j
Опр. Говорят, что это посл-ть обладает независимостью в совокупности, if для любой посл-ти Аi1,Аi2,…Аi k
P(Аi1,Аi2,…Аi k)= Р(Аi1)Р(Аi2)…Р(Аi k)
Св-во: Из независимости в совокупности Þ по парная независимость. Док-во: Достаточно положить в посл-ти А1, А2, …, Аn ; А1 = А1, А2 = А2, А3 = …=W; Р(А1, А2)=Р(А1)Р(А2). Доказано.
Обратное, вообще говоря, неверно.
Пример Бернштейна.
прав. тетраэдр. W={к,с,з,ксз}; Р(нижняя грань содержит красный свет)=Р(к)=Р(с)=Р(з)=2/4=1/2; Р(ксз)=1/4;
 Р(кс)=Р(сз)=Р(кз)=1/4;
Р(кс)=Р(сз)=Р(кз)=1/4;
а) по парная нез-ть: Р(кс)=Р(к)Р(с), т.е. ¼=½ · ½, т.е. верно б) нез-ть в совокупности: Р(ксз)¹Р(к)Р(с)Р(з), т.к. ¼=½ · ½ · ½, т.е. независимости в совокупности нет.
14 Независимость событий попарная и в совокупности. Пример Бернштейна
Независимость событ. Ех Бернштейна
Рассмотрим посл-ть событий А1, А2, …, Аn
Опр. Говорят, что эта посл-ть обладает попарной независимостью, if Р(АiАj)=Р(Аi)Р(Аj) " i¹j
Опр. Говорят, что это посл-ть обладает независимостью в совокупности, if для любой посл-ти Аi1,Аi2,…Аi k
P(Аi1,Аi2,…Аi k)= Р(Аi1)Р(Аi2)…Р(Аi k)
Св-во: Из независимости в совокупности Þ по парная независимость. Док-во: Достаточно положить в посл-ти А1, А2, …, Аn ; А1 = А1, А2 = А2, А3 = …=W; Р(А1, А2)=Р(А1)Р(А2). Доказано.
Обратное, вообще говоря, неверно.
Пример Бернштейна.
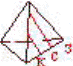
прав. тетраэдр. W={к,с,з,ксз}; Р(нижняя грань содержит красный свет)=Р(к)=Р(с)=Р(з)=2/4=1/2; Р(ксз)=1/4;
Р(кс)=Р(сз)=Р(кз)=1/4;
а) по парная нез-ть: Р(кс)=Р(к)Р(с), т.е. ¼=½ · ½, т.е. верно б) нез-ть в совокупности: Р(ксз)¹Р(к)Р(с)Р(з), т.к. ¼=½ · ½ · ½, т.е. независимости в совокупности нет.
17 Гипергеометрическое распределение.
Отличие от схемы бернули- выбор БЕЗ ВОЗВРАЩЕНИЯ
Дано 4- б;6-ч; Без возвращения взяли 4 шара А={среди 4-х есть 1б}
P(A)=?
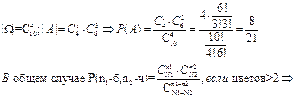
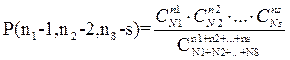
12 Формула полной вероятности
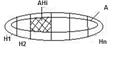 H1,H2,Hn-образуют конечное разбиение (полная группа) если
H1,H2,Hn-образуют конечное разбиение (полная группа) если
1 ![]()
2![]() i=j Hi-Гиподезы
i=j Hi-Гиподезы
ТЕОРЕМА:
Если H1,H2,Hn-образуют конечное разбиение,то
![]()
ДОК-ВО
A=A•Ω=A∑Hi=∑AHi;à
P(A)=P(∑AHi)=∑P(AHi)=∑P(Hi)•PHi(A)
Пример:
![]() N- белых шаров; M- черных.
Р(б.ш.)=N/(N+M)
N- белых шаров; M- черных.
Р(б.ш.)=N/(N+M)
Потерян шар неизвестного цвета. После этого вытаскивают шар. какова вер-ть, что он белый? А1={был потерян белый шар}; А2={потерян черный}; В={вытащить белый}
![]()
![]()
Р(В)=Р(В/А1)Р(А1)+ Р(В/А2)Р(А2);
Р(А1)=N/(N+M); Р(А2)=M/(N+M)
![]()
15 Схема Бернулли. Последовательность независимых испытаний
Пусть нек-ое случайное событие имеет 2 исхода. Ех, W={”О”,”P”} или W={²£2²,²³3²}. Назовем эти 2 исхода успехом и неудачей (У и Н) или (0 и 1). Допустим Р(У)=р, Р(Н)=q=1-р. Произведем наш эксперимент n - раз. Т.е. проделаем последовательность независимых испытаний. Исходы независимы.
![]()
Р(А1А2…An)=P(A1)P(A2)…P(An);
P(УУ…У)=рn; P(HH…H)=qn. Введем случайную величину mn равную числу успехов в n независ. испытаниях. Тогда:
P(mn=n)=рn;
P(mn=0)=qn. mnÎ{0,1,…,n}. Найдем P(mn=1): Р(УН…Н)= рqn-1; çAç=n. P(mn=1)= nрqn-1 по
классической схеме. В общем случае: P(mn=k)=![]()
pkqn-k - вер-ть тогo, что наблюдалась цепочка УУУ(k шт)ННН(n-k шт)Число таких цепочек, в к-ых k успехов, n-k неудач будет равно Ckn, т.е. столькими способами м. расставить k успехов по n местам. Если в одном эксперименте возможны 2 исхода, то говорят, что испытания проводятся по схеме Бернулли.
Ех, установлено, что Р(рожд.м)=0,51=р; Р(рожд. д)=0,49=q. Найти вер-ть того, что в наугад выбранной семье из 5 детей будет 3 мальчика. Р(m5=3)=С53p3q2=5!0,5130,493
18 Случайные величины дискретного типа. Распределение с.в
Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать графически, аналитически и таблично. Ряд распределения (таблица)- первая строка содержит возможные значения, а вторая их вероятности.
Многоугольник распределения; в прямоугольных координатах строят точки (Xi,Pi) а затем соединяют их отрезками прямых.
Пусть (W,L,Р) – вероятностное пространство. W - ПЭИ, L- алг. событий, R - вер. мера. Случайная величина – числовая ф-ция на W - x(w) такая, что " аÎR будет $ событие {w|x(w)=а}ÎL
Ех, правильная монета брошена 3 раза. Случайная величина x(w)- это кол-во выпавших орлов.
x(w1)=3, x(w2)=x(w3)=x(w4)=2, x(w5)=x(w6)=x(w7)=1, x(w8)=0.
Указать мн-во значений случ. величины это еще не все, необходимо указать соответствующие вер-ти. Когда все это сделано, то говорят о том, что определено распределение случ. величины x. Обычно распределение, if мн-во значений мало, задается в виде таблицы.
x
0
1
2
3
w
1/8
3/8
3/8
1/8
S=1
Пусть выпадение «О» – успех.
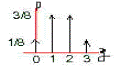 Р(x=0)=Р(w8)=Р(«РРР»)=Р(m3=0)=С30(1/2)0(1/2)3=1/8
Р(x=0)=Р(w8)=Р(«РРР»)=Р(m3=0)=С30(1/2)0(1/2)3=1/8
М. было и проще Р(w8)=1/çWç=1/8
19 Дискретные распределения. Примеры
Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать графически, аналитически и таблично. Ряд распределения (таблица)- первая строка содержит возможные значения, а вторая их вероятности.
1. Вырожденное распределение в т. а :
x
а
Rx
1
2. Распределение Бернулли
x~Вр (случ. величина x имеет распределение Бернулли с параметром р), р – вер-ть успеха.
x
0
1
Rx
1-р
р
3. Биномиальное распределение. x~В(n,p), где n – кол-во независимых испытаний, р – вер-ть успеха, x - кол-во успехов в n незав. испытианий. Р(x=k)=Cnkpk(1-p)n-k
x
0
1
…
n
Px
(1-p)n
np(1-p)n-1
…
pn
Частным случаем будет распределение Бернулли В(1,р)=Вр
4. Равномерное распределение на мн-ве {1,2,…,N}
x
1
2
…
N
Rx
1/N
1/N
…
1/N
5. Геометрическое распределение.
x
0
1
2
k
…
q=1-p
Rx
p
pq
pq2
pqk
…
![]()
6. Распределение Пуассона.
![]()
(x=Пl); m=0,1,…; l>0
22 Числовые характеристики дискретной с.в. Свойства дисперсии.
Опр. Дисперсией наз. Dx =M(x-Mx)2
Смысл Dx - это мера уклонения значений (разброс) с.в. от М.О.
Иногда пользуются другой
мерой: среднее квадратическое отклонение ![]()
x 0 1
Rx 1-p p
Мx=р; Dx=(0-р)2(1-р)+(1-р)2р=р(1-р)
I. р=0. 000…0. среднее арифмет. = 0 Dx=0
II. р=1, 111..1, сред.арифмет.=1, Dx=0
III. р=1/2, 00110110..01, сред.арифм.»1/2, Dx=1/4
1). Dx ³0 Док-во: Dx =M(x-Mx)2³0 (по св-ву 1)
2)![]()
Док-во: Пусть Mx =А, тогда
Dx=M(x-Mx)2=M(x2-2Ax+A2)
3). D(Ax+B)=A2Dx
Док-во: D(Ax+B)=M(Ax+B-M(Ax+B))2= M(Ax-AMx)2=A2Dx
4). if x и h независимы, то D(x+h)=Dx+Dh Док-во:
D(x+h)=M(x+h)2-(M(x+h))2=
![]()
![]()
Коэффициентом корреляции r
случайных величин X и Y называют отношение корреляционного момента к
произведению средних квадратических отклонений этих величин. ![]() (корреляционным моментом случайных
величин называют математическое ожидание произведения отклонений этих величин
(корреляционным моментом случайных
величин называют математическое ожидание произведения отклонений этих величин
![]() , среднеквадратичным
отклонением случайной величины называют квадратный корень из дисперсии)
(Св-ва: величина коэффициента кореляции не зависит от выбора единиц измерения
случайных величин. Коэффициент корреляции независимых случайных величин равен
нулю; абсолютная величина коэффициета корреляции непривышает единици)
, среднеквадратичным
отклонением случайной величины называют квадратный корень из дисперсии)
(Св-ва: величина коэффициента кореляции не зависит от выбора единиц измерения
случайных величин. Коэффициент корреляции независимых случайных величин равен
нулю; абсолютная величина коэффициета корреляции непривышает единици)
Две случайные величины X и Y называют коррелированными, если их корреляционный момент отличен от нуля; X и Y называют некоррелированными величинами, если их корреляционный момент равен нулю. Две коррелированные величины также и зависимы.
Среднеквадратичным отклонением случайной величины Х называют квадратный корень из дисперсии.
Модой М0 называют варианту которая имеет наибольшую частоту
Медианой ме называют
варианту, которая делит вариационный ряд на две части, равные по числу
вариант. Если число вариант нечетно, те n=2k+1
то ![]() при четном n=2k
медиана
при четном n=2k
медиана ![]()
Начальным моментом порядка к случайной величины Х называют математическое ожидание величины Х^к
Центральным моментом порядка к случайной величины Х называют математическое ожидание величины (X-M(X))^k
20 Индикатор и его свойства.
Выжной характеристика случайной величины является индикатор событий I{A}

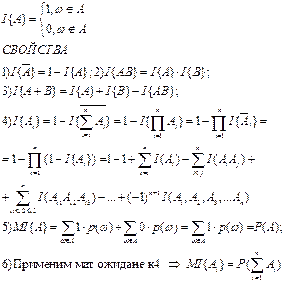
23 Независимость с.в. дискретного типа. Свойства м.о. и дисперсии
Случайные виличины ξ и η независимы если ддя любых К и I
![]() Свойства
Свойства
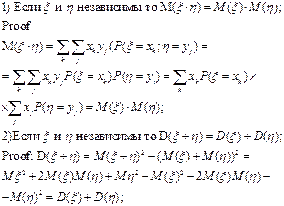
25 Геометрический смысл числовых характеристик. Уравнение регрессии
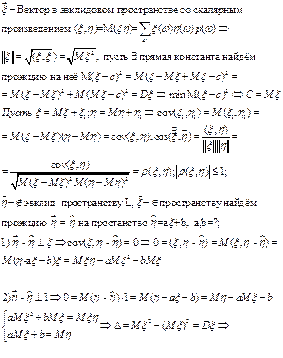
21 Числовые характеристики дискретной с.в. Свойства м.о
Путь имеется закон распределения с.в.:
w w1 w2
x х1 х2 …
Px р1 р2
Обычно ЭИ подразумеваются.
Опр. Математическим ожиданием (М.О.) дискретной с.в. наз. Число сумму произведений всех ее возможных значений
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.