Критерии устойчивости системы автоматического управления

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

ИАТЭ НИЯУ МИФИ

Кафедра АКиД

Лабораторная работа №3

Тема: «Критерии устойчивости САУ»

Обнинск

2013

Дано:

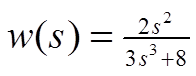
Сигнал:

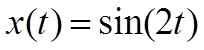
Задаем передаточную функцию в Scilab:

-->y=poly([0 0 2], "s","c")

y  =

2 

2s  

-->x=poly([8 0 0 3], "s","c")

x  =

3 

8 + 3s  

-->w=y/x

w  =

2   

2s    

------  

3 

8 + 3s  

-->s=syslin('c',w)

s  =

2   

2s    

------  

3 

8 + 3s  

Проверка устойчивости разомкнутой системы с помощью критерия Гурвица:

Считаем детерминант

-->det([0 8 0;3 0 0;0 0 8])

ans  =

- 192. 

Все элементы главного минора больше нуля, но детерминант меньше нуля, следовательно, система является не устойчивой по критерию Гурвица.

Проверка устойчивости замкнутой системы с помощью критерия Михайлова и следствия из него:

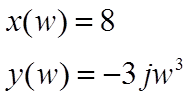
-->deff("u=re(w)","u=8")

-->deff("v=im(w)","v=-3*w^3")

-->x=re(0:0.1:2)

-->y=im(0:0.1:2)

-->plot(x,y)

-->xgrid()

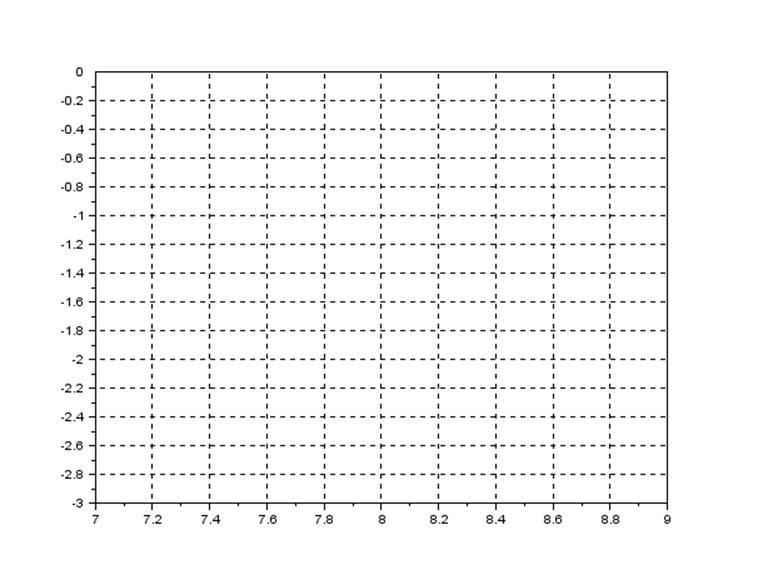
Следствие из критерия Михайлова:

-->xxx=roots(poly([8],"w","c"))

xxx  =

[]

-->yyy=roots(poly([0 0 0 -3],"w","c"))

yyy  =

0 

0 

0 

-->plot2d(xxx,[0 0],style=-1)

-->plot2d(yyy,[0 0 0],style=-3)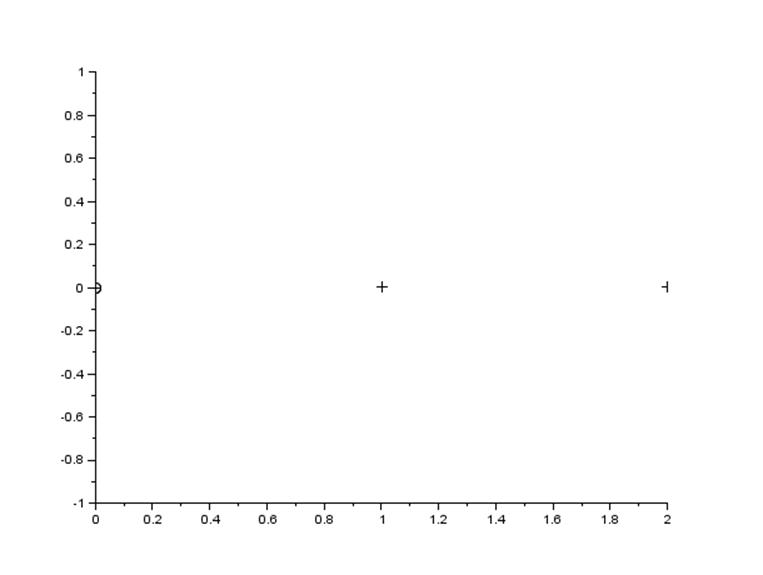

Корни не чередуются, что является следствием неустойчивости замкнутой системы

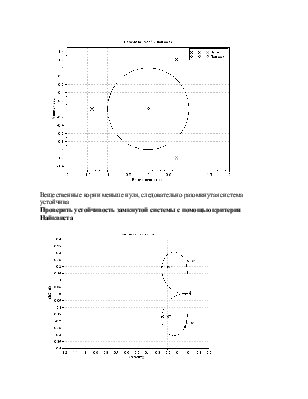
Найти полюса и нули передаточной функции разомкнутой системы и представить их графически

-->xxx=roots(numer(s))

xxx  =

0 

0 

-->yyy=roots(denom(s))

yyy  =

- 1.3867225             

0.6933613 + 1.200937i 

0.6933613 - 1.200937i 

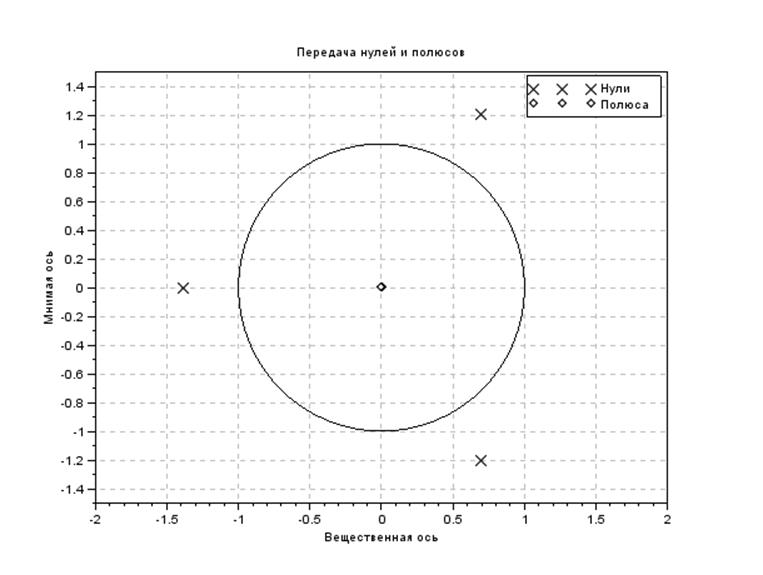
Вещественные корни меньше нуля, следовательно разомкнутая система устойчива

Проверить устойчивость замкнутой системы с помощью критерия Найквиста

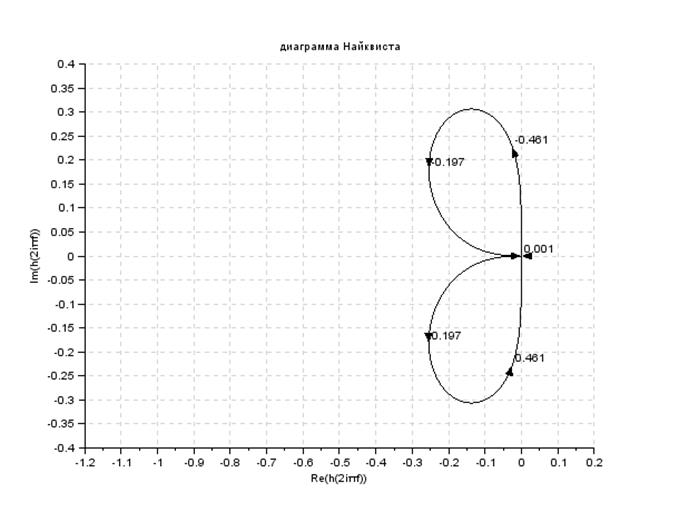
Так как доказано, что разомкнутая система устойчива, то замкнутая система является неустойчивой по критерию Найквиста, так как годограф не проходит через точку(-1;j0)

Проверить устойчивость замкнутой системы с помощью логарифмического критерия устойчивости

-->[jm,fr]=g_margin(s)

fr  =

[]

jm  =

Inf 

-->[pm,fr2]=p_margin(s)

fr2  =

[]

pm  =

[]

-->bode(s)

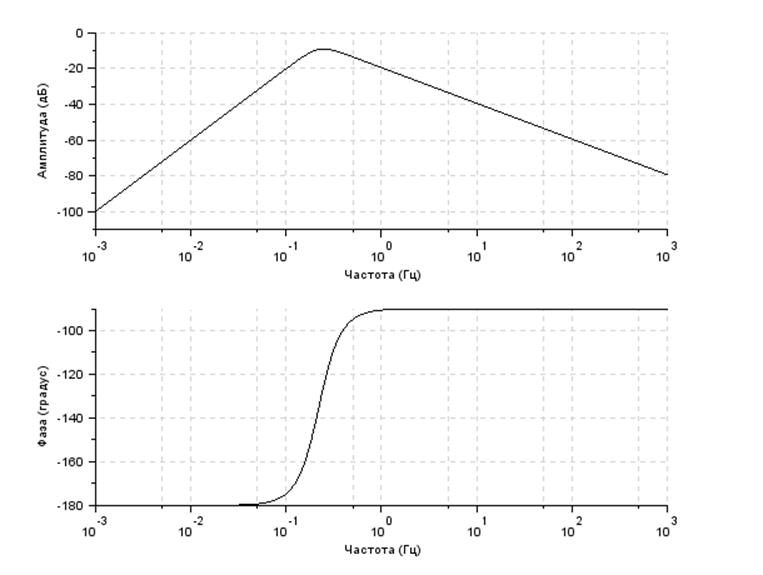
Нет запаса устойчивости ни по фазе, ни по амплитуде, следовательно замкнутая система неустойчива