Преобразования случайных величин. Применение полярных координат. Моделирование усеченных распределений

Следовательно, можно ввести дискретную случайную величину h с распределением

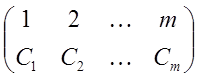   так, что P(h=k)=C_k.

Теорема 3. Пусть g₁ и g₂-независимые случайные числа. Если по числу g₁ разыграть  h=k,  затем из уравнения   определить x, то функция распределения x=F(x).

Доказательство: По формуле полной вероятности вычислим функцию распределения величины  x, построенной в теореме:

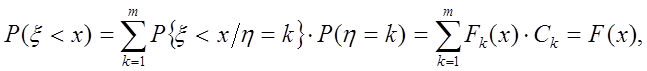ч.т.д.

Пример. Случайная величина x определена на 0<x<1 и имеет функцию распределения 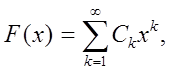   где все C_k³0.

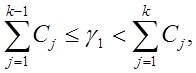Считаем, что . Тогда, если  то

Пример. Случайная величина x определена в 0<x<2 с плотностью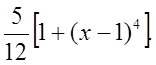

Если воспользоваться теоремой 2, то получим уравнение пятой степени, что не очень удобно. Воспользуемся методом суперпозиции.

Тогда на интервале (0,2) можно выделить плотность p₁(x)=1/2, тогда p(x)=(5/6)p₁(x)+(1/6)p₂(x), где p₂(x)=(5/2)(x-1)⁴ . Тогда получим явный алгоритм для моделирования x: x=2g₂, если g₁<5/6, и x= 1+(2g₂-1)^1/5, если  g₁>=5/6.

Упражнения:

1)   x равномерно распределена на (4;7).  Написать алгоритм моделирования сл.в. x.

2)    x имеет функцию распределения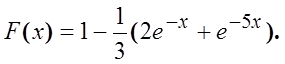

Вывести явную формулу для моделирования x.

3)   Смоделировать x на (0;l) с плотностью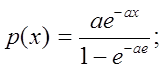

Преобразования вида         

-независимые случайные числа.

Извлечение корней из случайного числа

Пусть  x  имеет распределение F(x)=xⁿ при 0<x<1.

Тогда  x можно вычислить по формуле

Т.е. в любом алгоритме можно заменить извлечение корня из сл. числа взятием наибольшего из нескольких независимых сл. чисел.

Моделирование гамма распределения

Во многих задачах встречаются сл. в. x, распределенные на 0<x<¥ с плотностью вероятностей

p_n(x)=[(n-1)!]^-1x^n-1e^-x, n³1.

Такие распределения часто встречаются в теории надежности. При n=1 получаем экспоненциальное распределение. Тогда при любом n значения x⁽ⁿ⁾ можно вычислять по формуле x⁽ⁿ⁾=-ln(g₁g₂…g_n) - под знаком логарифма - произведение n сл. чисел.

Моделирование биномиальных распределений

Рассмотрим случайную величину x, которая подчиняется биномиальному распределению с параметром p:

P(x=k)=C_n^kp^k(1-p)^n-k,    k=0,1,…,n.

Это вероятность того, что при n экспериментах некоторое событие произойдет ровно k раз, если в одном опыте вероятность его появления равна p. Конечно, x можно моделировать по Теореме 1, но, чтобы не вычислять все вероятности p_k, можно воспользоваться следующим алгоритмом. Для каждого из чисел g₁,g₂,…,g_n проверяется неравенство g<p. Если это неравенство оказалось выполненным k раз, то  x=k.    Т.е. .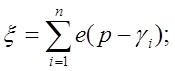

Приближенное моделирование нормального распределения

Рассмотрим сумму n независимых равномерно распределенных величин 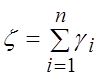,  Mz=n/2, Dz=n/12, тогда нормированная сумма  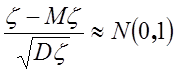, или   .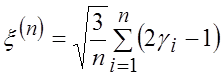

Согласно ЦПТ при n®¥ распределение x стремится к нормальному.

Нормированная сумма n независимых одинаково распределенных величин ~N(0,1):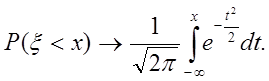     

Причем асимптотика устанавливается очень быстро. Для n=12

.

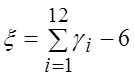Иногда ограничиваются лишь пятью слагаемыми, но зато добавляют поправку, которая ускоряет сходимость распределения к нормальному:       .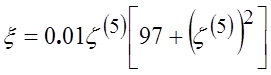

Методы отбора

Пусть в некотором пространстве          задана случайная точка с функцией распределения      и некоторой областью

Рассмотрим случайную величину

Чтобы вычислить x, надо выбрать    QÎG. Если QÎB ,то вычисляется x; если QÏB , то точка Q отбрасывается и выбирается новая.

Т.е., из случайных точек Q с функцией распределения   отбирают точки, принадлежащие   B, и по ним вычисляется x.

Формула            определяет метод отбора.

В начале курса мы рассмотрели пример, где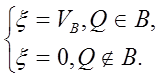

Эффективностью метода отбора называют вероятность отбора, или вероятность того, что точка Q будет использована для расчета  x, а не будет отброшена.

т.е. эффективность метода

Выбрав N точек Q, мы используем эффективность N точек для расчета x. Очевидно, чем > э(эффективность), тем лучше.

Моделирование усеченных распределений

Пусть     на (a,b):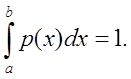

И пусть x имеет усеченное распределение  p₁(x) , если x распределена  на  (a`,b`)Ì(a,b) и ее плотность p₁(x) пропорциональна p(x).

Очевидно, что 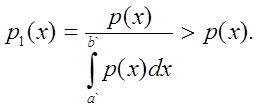 , т.к.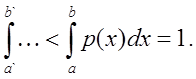

Если мы умеем вычислять  , то  x=h, если hÎ(a`,b`).

Например,               на  (0,¥)

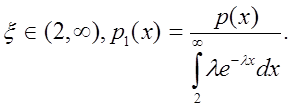
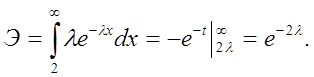
Очень просто  моделировать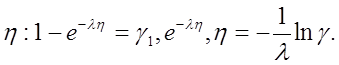

Тогда    x=h, если    h³2, при этом  эффективность=e^-2l.

Метод Неймана

Рассмотрим случайную величину  x   на (a;b) с p(x)£c:

Теорема 4. Пусть g₁   и  g₂  -независимые случайные числа,

Случайная величина x  определенная условием x=x¢, если h<p(x¢), имеет плотность вероятности p(x).

Доказательство: точка Q(x¢,h¢)~р.р. в квадрате (a<x<b, 0<y<c)   (ее плотность 1/c×(b-a)) 

Вычислим вероятность

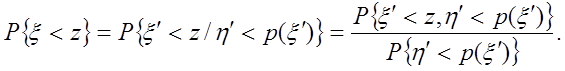- по построению в теореме.

Плотность т..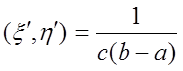

Знаменатель равен вероятности

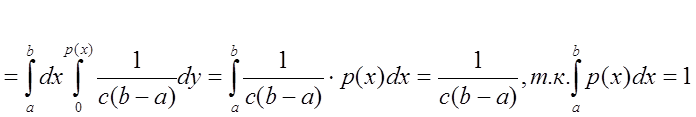
Числитель =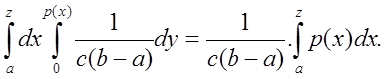

Т.е.,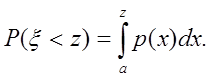 Что и требовалось доказать.

Эффективность метода Неймана  э=p(h¢<p(x))=1/c(b-a).

При выборе G для сложной области B следует стремиться к min G, т.к. э=пл.B/пл.G.

В данном методе следует выбрать c=sup p(x) на (a,b).

При выборе алгоритмов для расчета методами Монте-Карло различных задач необходимо выбрать преобразования для случайной величины x.

Однозначно порекомендовать что-то нельзя. Выбор зависит от различных факторов.

Если время на получение одного значения  x  стремится к min, то усложняется алгоритм (больше места или длиннее программа).

Быстрее всего работать с таблицей, но если качество одномерного распределения  g_i  хорошо проверено, то качество групп может быть хуже