


Задания на семинарские занятия
Семинар 1. Имитационное моделирование
Схема машинного эксперимента
Математическая схема как переход от содержательного описания проблемы к математической модели
Функциональная схема и Q-схема
Показатели эффективности системы
Статистическая оценка показателей эффективности
Статистическая устойчивость оценок
Семинар 2. Статистическое моделирование
Проверка функциональной и Q-схемы системы, заданной в курсовой работе (КР)
Временная диаграмма
Статистическое моделирование параметров модели системы
Задачи:
1. Смоделировать
случайную величину ξ, заданную рядом распределения (параметр с
найти): ξ :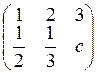 .
.
2. Смоделировать случайное событие появления бракованной детали, если вероятность брака равна 0,08.
3. Смоделировать наступление 2 независимых, но совместных событий А и В, вероятности наступления которых p(A)=0.7, p(B)=0.4.
4. Смоделировать наступление 3-х независимых событий А, В, С: Р(А)=0.6; Р(В)=0.8; Р(С)=0.9.
5. Смоделировать случайную величину, моделирующую путь обслуживания заявки, если с вероятностью 0,3 она пойдет на обработку в 1-ый канал, с вероятностью 0,5 - во 2-ой канал и с вероятностью 0,2 - в 3-ий.
Семинар 3. Статистическое моделирование
Проверка выполнения КР
Статистическое моделирование параметров модели системы
Задачи:
1.
Смоделировать случайную величину ξ с функцией распределения (параметры а
и b найти либо задать): Fξ(x)=x2-2x+1,
x![]() (a,b).
(a,b).
2. Смоделировать случайную точку Q, равномерно распределенную в кольце радиуса (R1, R2).
Семинар 4. Статистическое моделирование
Проверка выполнения КР
Статистическая устойчивость оценок
1.Смоделировать
случайную величину ξ с заданной плотностью распределения: fξ(x)=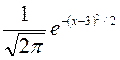 ,
x
,
x![]() (-
(-![]() ,
,![]() ).
).
2.Смоделировать
случайную величину ξ с заданной функцией распределения: Fξ(x)=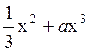 ,
x
,
x![]() (0,1).
(0,1).
3.Смоделировать
случайную величину ξ с заданной плотностью распределения: 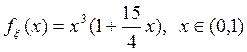 .
.
Семинар 5. Преобразования случайных величин
Проверка выполнения КР
Прием КР
Задачи:
1. Два равносильных противника играют в шахматы. Было сыграно четыре партии. Смоделировать случайную величину ξ - число выигрышей первого противника.
2. В среднем по 15% договоров страховая компания выплачивает страховую сумму. Смоделировать случайную величину ξ - число договоров из пяти, связанных с выплатой страховой суммы.
3. Производится залп из четырех орудий по некоторому объекту. Вероятность попадания в объект из каждого орудия равна 0,6. Смоделировать случайную величину ξ – число попаданий по объекту.
4. Смоделировать количество студентов, с первого раза сдавших экзамен по Моделированию систем, если для одного студента вероятность сдать экзамен равна 0.8. В группе 18 студентов.
Семинар 6. Вычисление интегралов методом Монте-Карло
Проверка выполнения КР
Прием КР
Задачи:
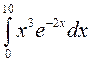 , используя
случайную величину ξ, задаваемую плотностью распределения fξ(x)~ e-2x.
, используя
случайную величину ξ, задаваемую плотностью распределения fξ(x)~ e-2x. 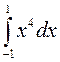 ,
fξ(x)~ x2.
,
fξ(x)~ x2.Семинар 7. Аналитические модели СМО
Проверка выполнения КР
Прием КР
Задачи:
Семинар 8. Аналитические модели СМО
Проверка выполнения КР
Прием КР
Задачи:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.