Методические указания к выполнению лабораторных работ по курсу “Моделирование систем” (Разработка генератора псевдослучайных чисел. Вычисление интегралов методом Монте-Карло)

Запись (4) означает, что m_n+1 равно остатку, полученному при делении gm_n на M ( или, другими словами,  m_n+1- это наименьший положительный вычет gm_n по модулю M). При некоторых g, M, m₀ получаются удовлетворительные последовательности, при других- плохие.

Удовлетворительная последовательность псевдослучайных чисел получается , например, при g=5¹⁷, M=2⁴², m₀=1.

Еще один пример алгоритма типа (2)     

γ_n+1=10^-kЦ(10^kД((1- γ_n)³10^k)),  например,  k=5.

Возможна также модификация метода вычетов путем прибавки к числителю некоторой константы

m_n+1=(gm_n+C) (mod M) .

Достоинства метода псевдослучайных чисел довольно очевидны. Во-первых, на получение каждого числа затрачивается всего несколько простых операций, так что скорость генерирования случайных чисел имеет тот же порядок, что и скорость работы ЭВМ. Во-вторых, программа занимает всего несколько ячеек накопителя. В-третьих, любое из чисел γ_k может быть легко воспроизведено. В-четвертых, нужно лишь один раз проверить качество такой последовательности, затем ее можно много раз безбоязненно использовать при расчете аналогичных задач.

Единственный недостаток метода – ограниченность количества псевдослучайных чисел, ибо, если последовательность чисел γ_0, γ_1,… γ_k… вычисляется на ЭВМ по формуле (1), то она обязательно периодическая. В самом деле, так как в коде любой ЭВМ можно записать лишь конечное число N чисел, заключенных между нулем и единицей, то рано или поздно какое-нибудь значение γ_L совпадет с одним из предыдущих значений γ_l . Тогда в силу (1)

γ_L+i= γ_l+i  при i=1,2,…                                              (5)

Пусть L- наименьшее число, удовлетворяющее (5) при некотором l (l<L). Множество чисел γ₀, γ₁,… γ_L-1 называется отрезком апериодичности последовательности (1), число L- длиной отрезка апериодичности, а P=L-l – длиной периода (рис.3)

Очевидно, что отрезок апериодичности состоит из различных чисел. И обычно для расчета не рекомендуется использовать больше, чем L чисел последовательности (1), т.к. это ведет к повторению испытаний в тех же условиях, что и раньше. Здесь увеличение числа реализаций не дает новых статистических результатов.

                                             P                                 P

0  1  2 … l  l+1   …            L-1 L…     …                                      i

L

Рис.3

Критерии проверки гипотез о законе распределения.

Случайные числа, полученные алгоритмическим способом, необходимо проверить на соответствие их предполагаемому закону распределения. Существует много критериев для такой проверки (критериев согласия):: критерий Колмогорова, критерий ω² и т.д. Каждый из них имеет свою область применения.

Принятие гипотезы о законе распределения по результатам проверки не является доказательством ее правильности. Это только означает, что экспериментальные данные не противоречат проверяемой гипотезе с точки зрения того частного критерия, который был применен.

Рассмотрим критерий χ²  (критерий Пирсона).

Критерий χ²  (хи-квадрат) имеет очень широкое распространение в практике статистических исследований. Он определяется формулой

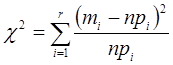                                         ,(6)

где r- количество интервалов гистограммы, построенной по статистическому материалу;

m_i – количество реализаций, попавших в i–ый интервал;

n – общее количество реализаций, содержащихся в экспериментальных данных;

p_i – вероятность попадания случайной величины в i–ый интервал:

p_i=F(x_i+1) – F(x_i),                                                      (7)

где F(x_i+1) , F(x_i) – значение теоретической функции распределения соответственно на правой и левой границах i-го интервала гистограммы.

При расчетах принимают

F(x₁)=0,

F(x_r+1)=1.

Пирсон показал, что при увеличении объема выборки выборочное распределение величины χ² стремится к распределению, задаваемому