
СМО с ограниченным временем ожидания
До сих пор мы рассматривали СМО с бесконечной очередью или с ожиданием, ограниченным длиной очереди (z<m).
На практике существуют СМО другого типа, где заявка, подождав некоторое время, может уйти из очереди (нетерпеливая заявка).
Рассмотрим марковскую СМО такого типа – M/M/n, очередь бесконечна, но время пребывания заявки в очереди £ Точ со средним значением `tоч. Тогда на каждую заявку, стоящую в очереди, действует как бы поток “уходов” с интенсивностью n=1/`tоч. Если этот поток – пуассоновский, то процесс в СМО – марковский.
Найдем вероятности состояний для стационарного режима в предположении, что такой режим существует. Граф состояний имеет следующий вид:
 l l l l l l l l
l l l l l l l l
… … …
m 2m 3m nm nm+n nm+rn
По схеме гибели и размножения, если существует стационарный режим, то
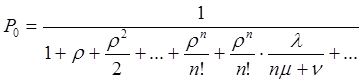 ====è обозначим b=n/m =è
====è обозначим b=n/m =è
=è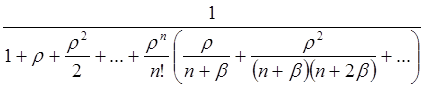 ,
,
Ряд в знаменателе сходится при любых положительных b и r. Значит, стационарный режим существует всегда.
Найдем характеристики эффективности такой СМО.
1. Относительная пропускная способность Q: обслужены будут все заявки, кроме тех, которые уйдут, не дождавшись. Тогда А=l-n×`r, где`r – среднее число заявок в очереди. Тогда Q=A/l=1-(n/l)×`r.
2. Среднее число занятых каналов`k=A/m=(l-n×`r)/m=r-b ×`r.
Видно, что при n®0 формулы превращаются в аналогичные с терпеливыми заявками.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.