Комплексные числа. Вещественные числа. Точная верхняя и точная нижняя грань. Свойства бесконечно малых последовательностей. Предельные точки последовательности

1.Комплексные числа (геометрическое представление, алгебраическая, тригонометрическая и показательная формы записи). Действия с комплексными числами

Положительные и отрицательные, в том числе иррациональные стали называть

действительными или вещественными. Сумма действительного и мнимого чисел называется комплексным числом   мнимая единица ‘i’ – мнимая единица                 

i²=  -1 y*i-чисто мнимое.

I)  алгебраическое определение К.Ч.

Z=x+iy . где x -действительная часть(Rez) y-мнимая часть(Imz)

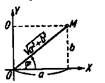II)  геометрическое определение К.Ч.

R=|oa|=|x₁²+y₁²|

Arg=ψ+2Π_k;Z=R(cosψ +isinψ) ψ=arctgy/x

e^iy=cosy+isiny. e^x+iy=e^x_*e^iy=e^x_* (cosy+isiny)=re^iψ

 

z1*z2=r1r2e^{i(ψ1+ ψ2)}    z1/z2=r1/r2e^{i(ψ1- ψ2)}

2) ФормулыМуавра.

(Z)ⁿ=rⁿe^inф =rⁿ(cosnф+isinф);

2.Вещественные числа. Точная верхняя и точная нижняя грань. Числовые последовательности. Сходящиеся последовательности. Свойства   произвольных   сходящихся   последовательностей.   Сходящиеся   в   несобственном   смысле последовательности

1)сверху

2)снизу

А =верхняя грань множества

НеограниченнаIf {х} ограничено справа и снизу то верхняя грань-Точная верхняя грань-sup{x};

M=sup if 1)M-верхняя грань;

2)

Точная нижняя грань-inf {x}; m=inf if 1)m-нижняя грань; 2)

Число, ’а’ называется пределом последовательности X_n-if

Сходящаяся последовательность имеет предел тогда и только тогда когда x_n = a + a_n.,

Теорема 3.7. Сходящаяся последовательность имеет только один предел.

Доказательство. Пусть а и b— пределы сходящейся последовательности {х_п}. Тогда, используя специальное представление (3.5) для элементов х_п сходящейся последовательности {х_п}, получим х_п = а + а_п, х_п = b+ b_п, где а_п и b_п — элементы бесконечно малых последовательностей {a_п} и {b_п}

Вычитая написанные соотношения, найдем а_п — |3_п = b— а. Так как все элементы бесконечно малой последовательности {а_п -b_п} имеют одно и то же постоянное значение b - а, то по теореме  b— а = 0, т. е. b = а. Теорема доказана.

Теорема 3.8. Сходящаяся последовательность ограничена.

Доказательство. Пусть {х_п} — сходящаяся последовательность и а — ее предел.

x_п = а+а_п, где а_п— элемент бесконечно малой последовательности. Так как бесконечно малая последовательность {а_п} ограничена то найдется такое число А, что для всех номеров п справедливо неравенство | а_п | <= А. Поэтому \х_п | <= | а | + А для всех номеров п, что и означает ограниченность последовательности {х_п). Теорема доказана.

Замечание. Ограниченная последовательность может и не быть сходящейся. Например, последовательность 1, —1, 1, —1,... ограничена, но не является сходящейся. В самом деле, если бы эта последовательность сходилась к некоторому числу а, то каждая из последовательностей {х_п — а} и {х_п+1 — а} являлась бы бесконечно малой. Но тогда, в силу теоремы 3.2, последовательность {(x_п — а) -(х_п+1 — a)} = {х_п — х_п+1} была бы бесконечно малой, что невозможно, так как | х_п — х_п+1 | = 2 для любого номера п.

Теорема 3.9. Сумма сходящихся последовательностей {х_п} и {у_n} есть сходящаяся последовательность, предел которой равен сумме пределов последовательностей {х_п} и {у_п}. Доказательство. Пусть а и b— соответственно пределы последовательностей {х_п} и {у_п}. Тогда х_п = а + а,_п,  y_n = b+p_n   {а_п }    (b_п)   - бесконечно малые последовательности, (х_п + y_п ) — (а + b) = а_п + b_п.

Таким образом, последовательность {(х_п + у_п) — (а + b)} бесконечно малая, и поэтому последовательность {х_п + у_п} сходится, и имеет своим пределом число, а + b.  

Теорема 3.10. Разность сходящихся последовательностей {х_п} и {у_п} есть сходящаяся последовательность, предел которой равен разности пределов последовательностей {х_п} и {у_п}

Теорема 3.11. Произведение сходящихся последовательностей {x_п} и {у_п} есть сходящаяся последовательность, предел которой равен произведению пределов последовательностей {х_п} и {у_п}.

Доказательство. Если а и b— пределы последовательностей {х_п} и {у_п} соответственно, то х_п = а + a_п, у_п = b+b_п и {x_п} *{у_п}=а-b + а*b_п + b-а_я + a_п*b_п. Следовательно,

{x_п} * {у_п} — a-b = а*b_п + b-а_я + a_п*b_п.следовательно бесконечно малая, и поэтому последовательность {х_п*у_п} сходится и имеет своим пределом число а*b

Лемма 1. Если последовательность {у_п} сходится и имеет отличный от нуля предел b, то, начиная с некоторого номера, определена последовательность {1/у_п }, которая является ограниченной.

Доказательство. Пусть е = | b|/2. Так как b<>0, то е > 0. Пусть N —номер, соответствующий этому е, начиная с которого выполняется неравенство \у_п — b \ < е или \у_п — b| < < | b|/2. Из этого неравенства следует, что при п>= N выполняется неравенство   | у_п | > | b|/2. Поэтому при п>=N имеем

|1/у_п|  следовательно, начиная с этого номера N, мы можем рассматривать последовательность {1/у_п }, и эта последовательность ограничена.

Теорема 3.12. Частное двух сходящихся последовательностей {Хп} и {у_п} при условии, что предел {у_п} отличен от нуля, есть сходящаяся последовательность, предел которой, равен частному пределов последовательностей {х_п} и {у_п}.

Доказательство. Из доказанной леммы 1 следует, что, начиная с некоторого номера