Ответы на экзаменационные вопросы № 1-22 по дисциплине "Физика" (Кинематика поступательного движения, Перемещение, путь, скорость, ускорение. Определение энтропии в статистической физике. Формула Больцмана)

период вращения – это время, за которое тело совершает один оборот: .

-угловое ускорение: .

Связь линейных и угловых характеристик.

Тангенциальное ускорение

Нормальное ускорение

Полное ускорение

Момент силы – это количественная мера взаимодействия тел, вследствие которого возникает вращательное движение.

, где  – это плечо силы.

Плечо силы – это кротчайшее расстояние от оси вращения до линии действия силы.

Момент инерции – это величина, которая характеризует распределение массы в теле и наряду с массой является мерой инертных свойств тела, проявляющихся в процессе его вращения.

Момент инерции материальной точки:  

твердого тела: , где - это расстояние от элемента массы до оси вращения.

однородного стержня:

обруча:

сплошного диска (цилиндра):

однородного шара:

Момент инерции тела относительно производной оси определяется по теореме Штейнера:                   , где  – это расстояние между данной осью, проходящей через центр масс тела.

Момент импульса - это величина характеризующая меру вращательного движения твердого тела или системы тел. Момент импульса равен произведению момента инерции твердого тела и его угловой скорости:                                                                                                                                                                – это основное уравнение динамики вращательного движения твердого тела.

Угловое ускорение вращательного тела прямо пропорционально суммарному моменту сил, действующему на него со стороны других тел, и обратно пропорционально моменту инерции этого тела.                                                                                                                                                                                      – это суммарный момент сил , действующих на вращающее тело со скоростью других тел, равен быстроте изменения момента импульса этого тела  и сонаправлен с вектором изменения момента импульса тела .

7.  Кинетическая энергия и работа при вращательном движении. Закон сохранения импульса. Гироскоп.

Работа силы при вращательном движении равна произведению момента силы на угол поворота тела. 

Кинетическая энергия материальной точки равна:

Здесь  – это момент инерции -той точки,

Кинетическая энергия всего тела слагается из кинетических энергий всех его материальных точек.

Таким образом, кинетическая энергия вращающегося твердого тела равна:

Кинетическая энергия вращающегося тела равна половине произведения его момента инерции и квадрата угловой скорости.

Согласно основному уравнению динамики вращательного движения момент силы, действующей на движущуюся по окружности вокруг некоторого центра материальную точку, равен быстроте изменения момента импульса этой точки.

Если , то  и , следовательно

Вывод: если момент сил, действующих на материальную точку, равен нулю, то момент импульса этой материальной точки остается неизмененным.

При ; 

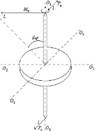
- прецессия

Прецессия – это вращение оси гироскопа вокруг основной оси.

S – южный магнитный полюс

N – северный

 – возмущающий момент силы

8.  Постулаты СТО. Преобразование Лоренца. Следствия из преобразований Лоренца.

Постулаты:

1)  Принцип относительности выполняется в инерциальных системах отсчета не только для механических явлений, но и для всех физических явлений и процессов.

2)  Скорость света в вакууме не зависит от движения источников света, являются постоянной величиной СТО – (специальная теорема относительности) не отвергает принципы относительности Галилея и преобразования Галилея, но расширяет эти понятия.

Из преобразований Лоренца возникает, что понятие временного и пространственного промежутка относительны и отличаются для разных инерциальных систем отсчета. Преобразования Лоренца:

          

,  

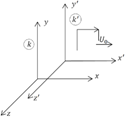
Следствия из преобразований Лоренца:

Сокращение длины.

Пусть в системе  тело(стержень) покоится с координатами  , для определения длины стержня в один и тот же момент времени испускается световой сигнал выходящий из системы  и фиксирующийся в системе  равна:

т.е. 

Преобразование промежутков времени: пусть в системе отсчета в одной и той же точке с координатами  происходят два события , тогда, в системе отсчета относительно которой происходит движение  временной интервал между событиями будет равен :   ;  ;  ;  .

9.  Преобразование и сложение скоростей в СТО.

Компоненты скорости  частицы в системе  определяются выражениями:

;  ;  ;

В системе  компоненты скорости  той же частицы равны:

;  ;  ;

Найдем формулы связывающие не штрихованные компоненты скорости со штрихованными, воспользовавшись преобразованиями Лоренца:

;  ;  ;   

Разделив первое равенство на четвертое получим:

;  ;

По полученным выше формулам осуществляем преобразования скоростей