НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
_____________________________________________________________________
основ радиотехники (ТОР)
РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И СИГНАЛЫ
ЗАДАНИЕ № 3
ЗАКОН РАСПРЕДЕЛЕНИЯ
СТАЦИОНАРНОСТЬ И ЭРГОДИЧНОСТЬ
Факультет: РЭФ
Группа: РТ5-24
Студент: Гринь И.А.
Дата сдачи «17» мая 2004 г.
Преподаватель: Курилин И.В.
Закон распределения.
Стационарный случайный процесс U(t) описан плотностью вероятности W(u); параметры функции W(u) приведены ниже.
Требуется:

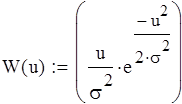
Параметры:
a=1.2 b=2.8 σ=2
1.Выражения для функции распределения F(u).
По определению функция распределения определяется следующим образом:
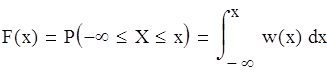
где ![]() -
плотность функции распределения.
-
плотность функции распределения.

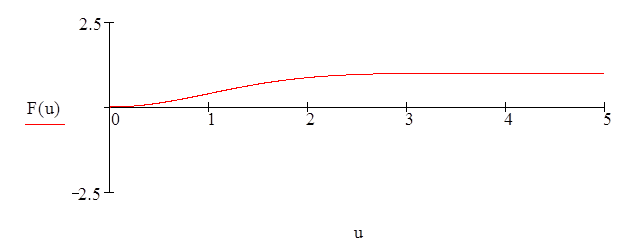
2. Выражение для характеристической функции
По определению характеристическая функция определяется следующим образом
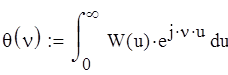
3. Энтропия
Так как у нас нормальный закон распределения то следует что энтропия будет вычисляться по формуле
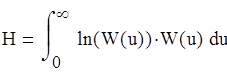
По определению энтропия характеризует меру неопределенности системы
![]()
Моментные функции. Стационарность и эргодичность.
Задан процесс Z(t).
Требуется:
Где ![]() и
и ![]() - детерминированные функции времени,
описываемые при помощи постоянных параметров
- детерминированные функции времени,
описываемые при помощи постоянных параметров ![]() и
и ![]()
X и Y - некоррелированные
случайные величины с известными математическими ожиданиями ![]() и
и ![]() и
дисперсиями
и
дисперсиями ![]() и
и ![]() , и
автокорреляционными функциями
, и
автокорреляционными функциями ![]() и
и ![]() .
.
![]()
![]()
1. Определение Математического ожидания процесса
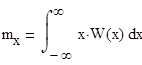
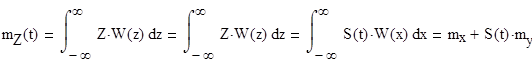
в силу некоррелированности величины X в силу того что функция S(t) детерминированной, то есть конкретно определенная на каком-то интервале времени
2. Определение дисперсии процесса
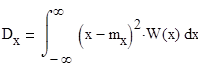
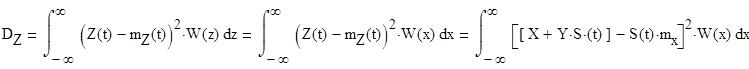
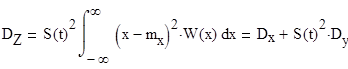
3.
Определение корреляционной функции![]()
Запишем исходный процесс в виде
![]()
где ![]()
Тогда
![]()
Распишем каждое слагаемое по отдельности:

![]()
![]()
так как не зависит от положения
![]()
![]()
![]()
![]()
так как ![]() и
и ![]()
не зависят от положения ![]() , то
, то ![]()
![]()
в силу свойств математического ожидания и некоррелированности величин
![]()
![]()
![]()
где ![]()
4. Проверка на условие стационарности процесса
![]()
из данного выражение видно что математическое ожидание зависит от времени, то есть первое условие стационарности не выполняется
![]()
где ![]()
Второе условие стационарности тоже не выполнено так как ковариционная функция зависит от положения времени отсчетов.
Дальнейшая проверка необязательна так как если первые два из условий стационарности не выполнены то процесс не стационарен во времени.
Данный процесс на эргодичность можно не проверять так как не выполнено первые два условия стационарности то есть процесс не стационарен и не эргодичен.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.