Определение математического ожидания, дисперсии и корреляционной функции процесса

Министерство образования и науки Российской Федерации

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

_____________________________________________________________________

                                                                      Кафедра теоретических

                                                                      основ радиотехники (ТОР)

РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И СИГНАЛЫ

ЗАДАНИЕ № 4

1.  Закон распределения

Стационарный случайный процесс  описан плотностью вероятности ;

Требуется:

а)  получить выражение для функции распределения ;

б) построить график ;

в) найти выражение для характеристической функции  и энтропии .

Плотность вероятности задана функцией:

 

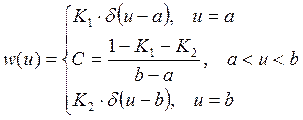
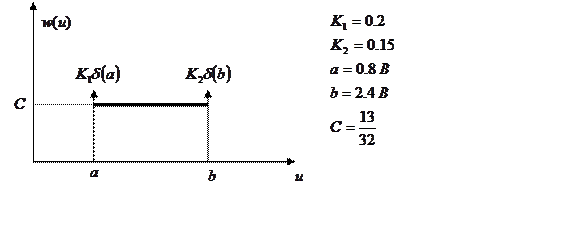
Получим выражение для функции распределения , для этого проинтегрируем функцию :

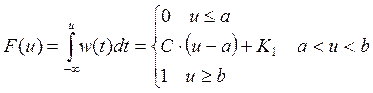
Построим график функции :

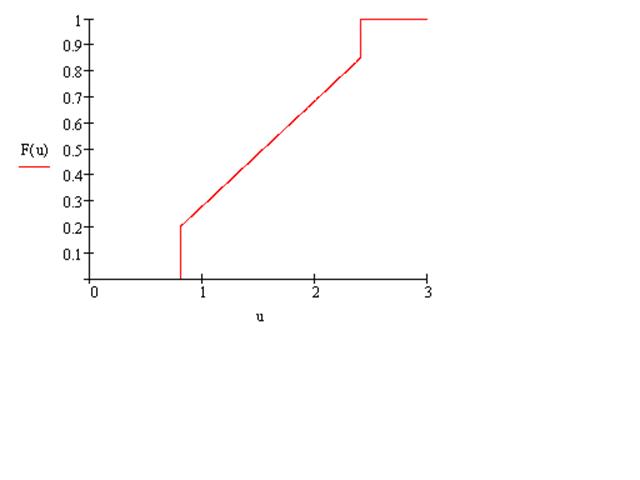
Найдем выражение для характеристической функции :

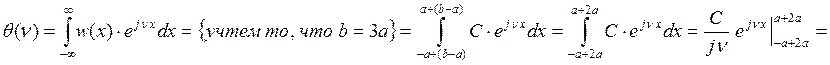
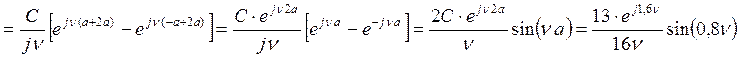
Найдем значение энтропии :

2. Моментные функции. Стационарность и эргодичность

При описании  приняты следующие обозначения:

 и  - детерминированные функции времени, описываемые с помощью постоянных параметров , , , ,  и ;

 и  - некоррелированные случайные величины с известными математическими ожиданиями  и  и дисперсиями  и ;

 и  - некоррелированные эргодические случайные процессы, которые соответственно имеют известные математические ожидания  и , дисперсии  и  и автокорреляционные функции  и .

Требуется:

а) определить математическое ожидание , дисперсию  и корреляционную функцию  процесса ;

б) классифицировать процесс  по признакам стационарности и эргодичности.

Дано:

Определение математического ожидания:

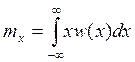
в силу некоррелированности величин  и  и в силу того, что функция  детерминирована (т.е. конкретно определена на каком-то интервале времени), а также в силу свойств математического ожидания получаем:

 (1)

Определение дисперсии:

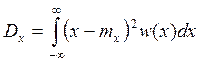
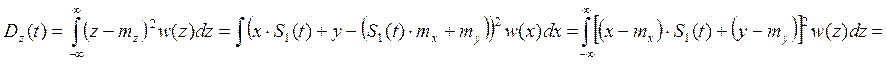
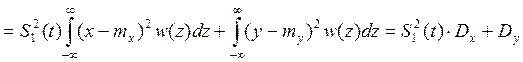
 (2)

Определение корреляционной функции :

Запишем исходный процесс в виде

где

тогда

Распишем каждое слагаемое по отдельности:

аналогично находим :

т.к. ВКФ  и  не зависят от положения и , то , где

В силу свойств математического ожидания и некоррелированности величин получим:

 (3)

Проверка процесса на условие стационарности и эргодичности:

Из выражений (1), (2) и (3) видно, что математическое ожидание и дисперсия зависят от времени, а автокорреляционная функция  зависит от положения  и . Значит исследуемый процесс не является стационарным. Проверка процесса на эргодичность не требуется, т.к. не выполняются условия стационарности.

Процесс не стационарен и не эргодичен.