Расчёт при оценке экологической ситуации. Моделирование в экологии, страница 4

для n=3, число опытов N=2³=8+k; (для данного случая число k=g+1, где g=6,
тогда N=8+7=15);

для n=4, число опытов N=2⁴=16+k; (для данного случая число k=g+1, где g=8,
тогда N=16+8=25);

для n=5, число опытов N=2⁵=32+k; (для данного случая число k=g+1, где g=10, тогда N=32+10=42);

    Подобные планы эксперимента называют полным факторным планом второго порядка.Способ построения матрицы 2ⁿ ясен (см. таблицу), где каждая из таблиц получается достроением матрицы 2^n-1. Такого типа матрица (для двух факторов) представлена в табл. 16. А план 2² позволяет сделать расчёт всех коэффициентов модели независимо один от другого

Таблица 16

Матрица центрального композиционного рототабельного
униформ–планирования второго порядка, n=2

Номер опыта u	Xo	X1	X2	X1 X2			Отклик
План 22
1	+1	–1	–1	+1	+1	+1
2	+1	–1	+1	–1	+1	+1
3	+1	+1	–1	–1	+1	+1
4	+1	+1	+1	+1	+1	+1
Звёздные и центральные точки
5	+1	+1,414	0	0	+2	0
6	+1	–1,414	0	0	+2	0
7	+1	0	+1,414	0	0	+2
8	+1	0	–1,414	0	0	+2
9		0	0	0	0	0

    Порядок использования расчётных формул для плана типа 2ⁿ:

1.  Кодирование переменных ;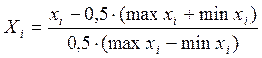

2.  Оценка дисперсии воспроизводимости на основании параллельных опытов 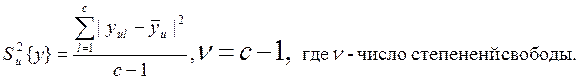 Каждый из N опытов повторяется c>1 раз и повторяется в центре эксперимента ,

3.  Проверка однородности дисперсии воспроизводимости  .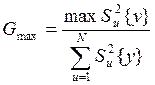

    Полученные значения G_max сравниваются с критическим значением критерия G_n1,n2,a (справочные таблицы критических значений G – критерия наибольшей эмпирической дисперсности к сумме эмпирических дисперсии; для a=0.05) для n₁=с–1, n₂=N(c–1) и уровнем значимости a. Если G_max<G_n1,n2,a, дисперсии считаются однородными с надёжностью (1–a). Для дальнейших расчётов принимается оценка дисперсии воспроизводимости

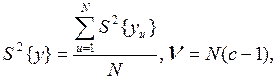 т.е. дисперсия усредняется.

    Если опыты повторялись только в центре эксперимента, то оценка дисперсии воспроизводимости будет следующей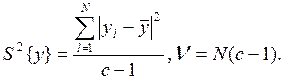

4.  Расчёт коэффициентов модели

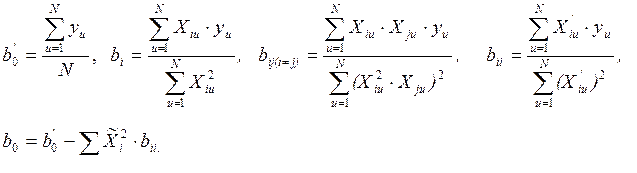
5.  Оценка дисперсии погрешности («ошибки») определения коэффициентов модели
(дисперсии коэффициентов различны)

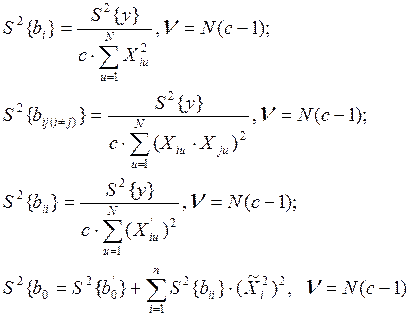
6.  Оценка критического значения коэффициента, где устанавливается доверительный интервал ,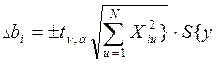

где -табличные значения -критерия Стьюдента с n=N-1;

a - уровень значимости (см. табличные критических значений критерия G). Если .

7.  Расчёт дисперсии неадекватности модели 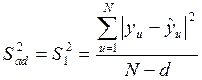, характеризующая разброс экспериментальных  относительно , предсказанных по уравнению регрессии. Число степеней свободы дисперсии  равно N-1, а дисперсии  равно , где d число членов уравнения регрессии.

8.  Составление и оценка значимости отношения дисперсий неадекватности и воспроизводимости (табл. значения). Для проверки адекватности уравнения регрессии составляется дисперсия неадекватности  с дисперсией воспроизводимости :  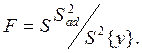Гипотезе об адекватности уравнения регрессии соответствует условие: , где  - критическое значение F-критерия (см. таблицу критериев); a - уровень значимости, при числе степеней свободы .

    Во многих задачах исследователь априорно предполагает, что при моделировании процесса (процессов) достаточно ограничится линейной моделью или моделью с линейными членами и частью возможных взаимодействий. Особенно типичная такая ситуация для многофакторных (более 4-х) задач, где полиномом второй степени обычно удаётся описать почти стационарную область, где предположительно находятся экспериментальные значения. Здесь уместно отметить следующее:

·  чем больше величина n, тем меньше обычно объём априорной информации;

·  маловероятно влияние тройных и более взаимодействий факторов;

·  на первой стадии многофакторного эксперимента обычно только намечается направление движения к оптимуму и достаточно аппроксимировать исследуемую часть поверхности отклика отклика y (x_i) плоскостью

·  с ростом n быстро возрастают сроки и стоимость эксперимента

    Внедрение результатов. Заключительный результат системного анализа представляет собой применение на практике результатов, полученных на предыдущих этапах. Если исследования по описанной выше схеме проведены удачно, то практические шаги, которые необходимо предпринять будут очевидны. В тоже время может выявиться неполнота тех или иных результатов или необходимость их пересмотра, в результате чего придётся корректировать модель и снова пройти какие–то из завершённых этапов.