Расчёт при оценке экологической ситуации. Моделирование в экологии, страница 3

1.  запас воды в водохранилище в момент времени (t) и его изменение с течением времени – объём водохранилища – V, млн. куб. метров в месяц;

2.  количество выловленной рыбы при рыбоводстве – «рыба», усл. тон в месяц;

3.  показатели загрязнения воды g – показатель превышения ПДК в водоёме, отн. един.;

4.  показатель кислотности (щёлочности) по рН;

5.  получение электроэнергии – ГЭС, млн. кв. часов в месяц;

6.  урожай собранной сельскохозяйственной продукции при искусственном орошении – С/х, усл. тонн в месяц.

    Далее необходимо выделить основные факторы, которые оказывают влияние на свойства водохранилищ:

·  приток по реке, на которой построено водохранилище (или несколько водохранилищ);

·  пополнение запасов воды за счёт боковых притоков и дождей;

·  убыль воды за счёт фильтрации воды в нижнем створе водохранилища и испарения;

·  вода расходуется на нужды сельского хозяйства;

·  коммунальное водоснабжение;

·  часть воды пропускается через плотину далее по реке, в том числе для получения электроэнергии.

    Схематически динамику запаса воды в водохранилище можно представить так, как показано на рис. 13.

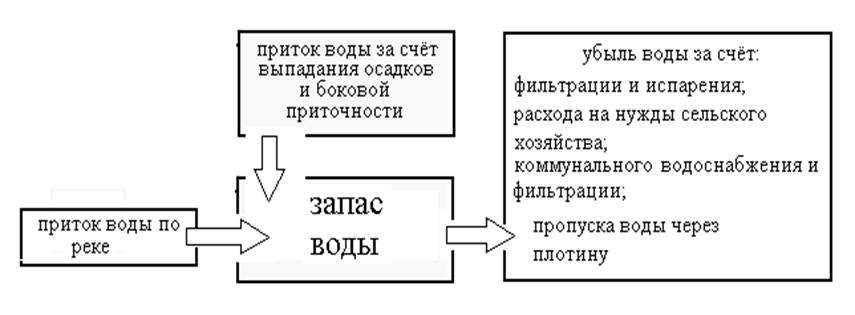
Рис. 13. Схема процессов определяющих запас воды в водохранилище

    Естественно предполагать, что запас воды в водохранилище не должен становится меньше некоторой величины, но и не должен превышать некоторого объёма водохранилища и как этот показатель будет изменятся во времени?

    Приток воды по реке, за счёт дождей и боковой приточности определяется по ежегодным наблюдениям (мониторингу) на протяжении ряда лет (как правило, 15–17 лет). Убыль воды – величина регулируемая (кроме фильтрации и испарения) и определяется хозяйственными потребностями. Фильтрация и испарение, как и приток по реке, также фиксируются многолетними наблюдениями.

    Выбор путей решения задач. Здесь можно выбрать несколько путей решения проблемы. Но всегда предпочтение отдаётся тем методам, которые позволят наиболее полно и эффективно использовать результаты аналогичных задач и соответствующий математический аппарат. При этом выбор тех или иных методов нередко зависит от специалистов (специалиста), при помощи которых и решается данная проблема.

    Моделирование и оценка возможных стратегий. Здесь следует отметить, что, моделируемым процессом, а также механизмам обратной связи присуща внутренняя неопределённость.

    Для решения данной задачи необходимо получить модель данной системы и использовать её для анализа работы экологического объекта.

    Планы первого и второго порядков. Полный факторный эксперимент
типа 2ⁿ. Ортогональное и рототабельное центральное композиционное планирование второго порядка. Рассматриваемые планы являются симметричными относительно центра «эксперимента» и ортогональными (симметричными) или рототабельными (добавление некоторого числа опытов в центре), т. е. факторы варьируются на двух уровнях (+1 и –1), где выполняется условие нормировки

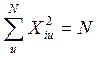, где по формуле кодирования ,

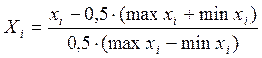где переменные  – кодированные значения переменных (исследуемых факторов) и они равны =+1 или –1 (часто цифру в этом случае опускают) и матрица плана состоит из Nстрок с сочетаниями знаков (+) и (–);  – натуральные значения переменных (исследуемых факторов).

Например, для двух факторов матрица планирования имеет вид (табл.14).

Таблица 14

Матрица плана 2²

Номер опыта	Переменные				Отклик Yu
	X0	X1	X2	X1X2
1 2 3 4	+1 +1 +1 +1	-1 +1 -1 +1	-1 -1 +1 +1	+1 -1 -1 +1	Y1 Y2 Y3 Y4
Проверка		0	0	0
		4	4	4

    Проверка условий ортогональности, например, для столбцов  и  выглядит следующим образом:

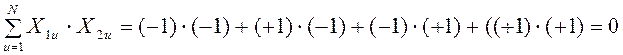 и т. д.

    При ортогональном центральном композиционном плане второго порядка расположение точек планов для двух и трёх факторов выглядит следующим образом (рис.14.).

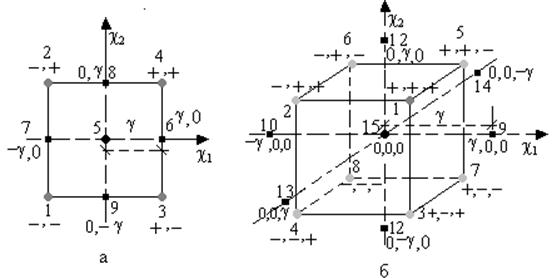Рис.14. Расположение точек центральных композиционных планов
 второго порядка для двух (а) и трёх (б) факторов

    Величина звёздного плеча g равна 1.00 для n =2, 1.215 для n=3 и 1.414 для  n=4. Ортогональность плана достигается специальным преобразованием квадратных переменных и выбора величины плеча g. В самом деле, если =±1, то =+1 и столбцы  и  не ортогональны. Поэтому при расчёте коэффициентов регрессии в колонку  записывается преобразованная переменная

,

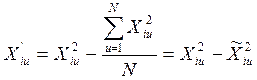Например, при n=2 вместо  записывается: в первом опыте , и т.д., а в девятом опыте  и т.д.

    Кроме того, в приведённой матрице (табл. 15.) представлены все возможные сочетания полного факторного эксперимента от 2² до2⁴.

Таблица 15

Фрагмент матрицы полного факторного эксперимента

 

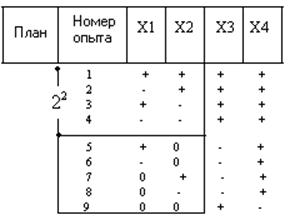    В матрице приведены все возможные сочетания 2, 3 и 4 факторов. Для n=2, число опытов равно 2²=4+k, где k равно числу звёздных точек g и один опыт по средине;