Способы отражения информации на тематических картах

Контрольная работа

Способы отражения информации на тематических картах

Цель работы: научиться использовать способы картодиаграмм  и картограмм для показа на тематических картах абсолютных суммарных и относительных характеристик  количественных показателей явлений в пределах заданных границ территориального деления.

Задание 1. Способом картодиаграмм показать на карте статистические данные по темам, приведенным в приложениях 1 и 2.

Методические указания: методику выполнения задания рассмотрим на примере составления карты «Медицинское обслуживание» для Центрально-Черноземного района. Тема картодиаграммы «Число врачей по областям».

Таблица 1.1

Области	Число врачей, чел.
	Всего	На 10 000 чел. населения
Белгородская	5104	35,9
Воронежская	10 477	42,2
Курская	5443	40,7
Липецкая	4465	36,0
Тамбовская	3935	29,9

1. Выписать из табл. 1.1 показатели в порядке возрастания, например: 3935; 4465; 5104; 5443; 10 477.

2. Разработать шкалу для картодиаграммы. Для этого следует построить график распределения показателей (гистограмму). По горизонтальной оси отложим одинаковые отрезки по числу показателей (в примере их пять); по вертикальной оси – величины показателей в удобном масштабе (рис. 1.1). По перегибам ступеней выделим границы интервалов шкалы и три градации (в тыс. чел.):

I ... 3900 – 4500

II ... 5100 – 5500

III … 10 477

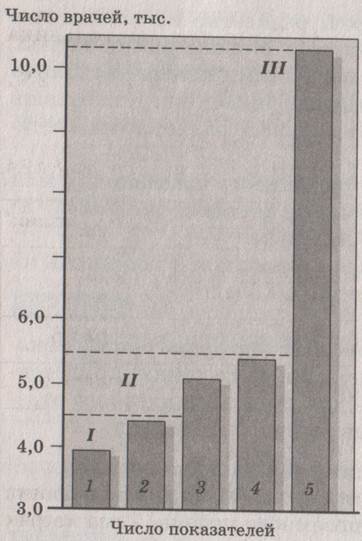К градации I относятся Тамбовская и Липецкая области, к градации II – Белгородская и Курская области, к градации III – Воронежская область.

3. Найти среднее значение (тыс. чел.) показателя в каждой градации (можно округлить их):

I ... 4200

II ... 5273

III ... 10 477

4. Выбрать фигуру для диаграммы и рассчитать размеры ее для каждой градации. Обычно ставится условие пропорциональности площади фигуры и показателя.

Рисунок 1.1 - Гистограмма для картодиаграммы

 

Можно выбрать круг, тогда его площадь  принимается за величину среднего для градации показателя и рассчитываются радиусы кругов: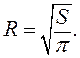

Если в качестве диаграммы взять квадрат, то  Тогда сторона

Если использовать треугольник, то 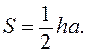 Здесь следует выбрать для всех градаций один размер основания а и рассчитать для каждой градации высоту треугольника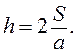

При использовании прямоугольников (), как и в предыдущем случае, выбирают одно основание а, тогда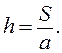

Для того чтобы треугольники и прямоугольники имели более компактную фигуру, можно задаться разными соотношениями а и h, например: 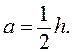 Тогда для треугол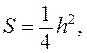ьника   для прямоугольника 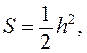  После определения высоты h находим значение а.

Полученные результаты сведены в табл. 1.2.

Таблица 1.2

Круг	Квадрат	Треугольник*	Прямоугольник*

* При основании 5 мм.

Полученные значения следует проанализировать, сравнив их с размерами регионов на карте, и выразить в миллиметрах или сантиметрах. Если эти значения большие, их можно уменьшить в одинаковое число раз для всех регионов (табл. 1.3).

Таблица 1.3

Круг	Квадрат	Треугольник*	Прямоугольник*

* При основании 5 мм.

Известно, что читаемость и наглядность карты зависят от художественного вкуса и грамотности ее автора. Сравним, как выглядят на карте рассмотренные фигуры (рис. 1.2), и выберем одну из них.

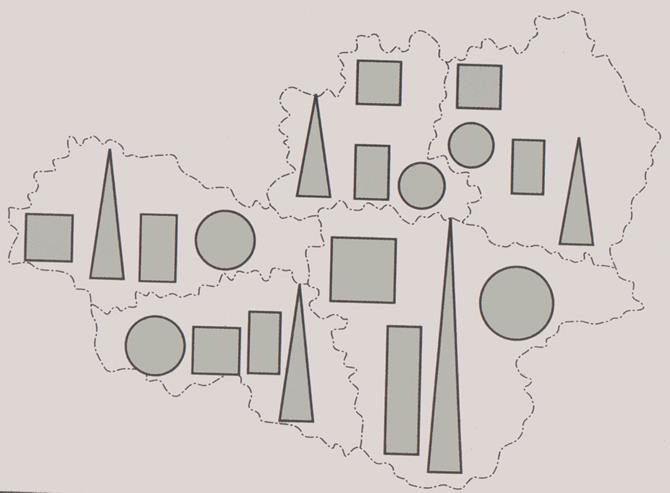
Рисунок 1.2 –  Пример использования в качестве диаграммы кругов, квадратов, треугольников и прямоугольников

Для определения размеров диаграмм можно использовать и условную шкалу. В этом случае также исходят из средних показателей по градациям.

По статистическим данным табл. 1.1 построим условную шкалу кругов. На прямой на произвольном расстоянии построим два круга – маленький и большой. Радиусы их выберем в соответствии с площадями районов и показателями. Маленький круг – диаграмма для градации I, большой – для градации III (рис. 1.3). Остается рассчитать размер круга для промежуточной градации II.

Разность между градациями I и III:

тыс. чел.

Эта разность на рис. 1.3 соответствует, например, 10 тетрадным клеткам.

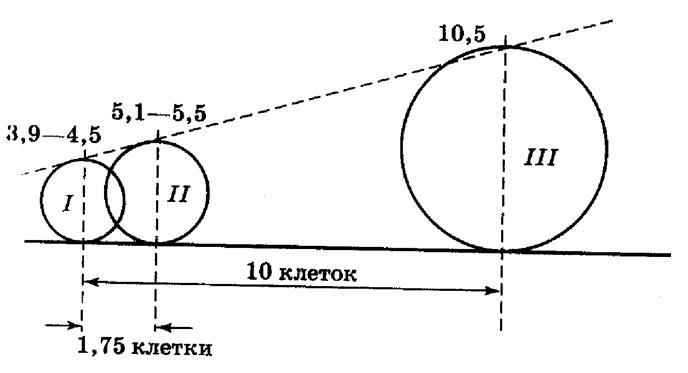
Рисунок 1.3 – Условная шкала

Разность между градациями I и II:

тыс. чел.

Вычисляем расстояние между центрами кругов градаций I и II из пропорции:

6,3 тыс. чел.	–	10 клеток
1,1 тыс. чел.	–	х

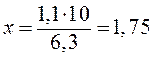 клетки.

Следовательно, второй круг должен располагаться на расстоянии 1,75 клетки от первого круга.

5. Вписать выбранные фигуры соответствующих размеров в границы районов.

6. Если требует задание, разделить фигуры на части пропорционально их количественным показателям.

7. Оформить легенду для картодиаграммы (рис. 2.1).

Задание 2. Способом картограммы показать на карте заданные относительные показатели явления. Исходные данные для выполнения задания и темы по вариантам приведены в приложениях 1, 2.

Методические указания. 1. Вычислить относительные показатели по районам. Например: для вычисления числа врачей на 10 000 жителей общее число врачей в районе разделить на численность населения и умножить на 10 000. Выписать полученные данные по возрастанию величин.