Проектирование отапливаемого здания термического цеха (пролет здания - 36 м, длина задания - 96 м, место строительства - г. Челябинск)

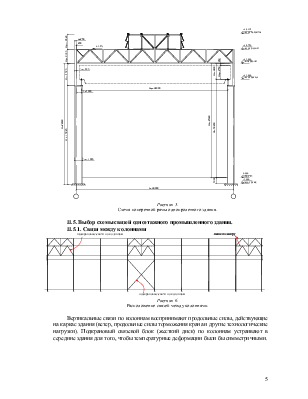
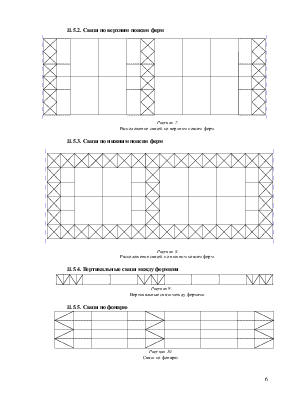
Требуемая ширина полки с учетом раннее принятой толщины t_f = 32 мм составит:

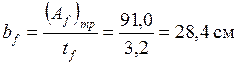, принимаем b_f = 30 см.

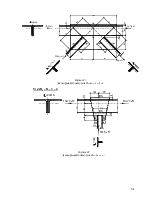
Получим следующее сечение:

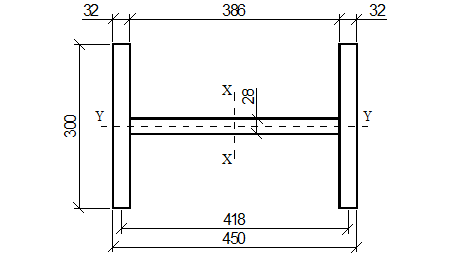
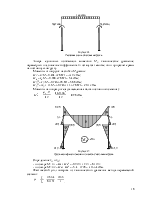
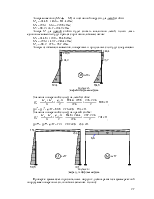
Рисунок 59.

Сечение верхней части колонны.

Подобранное сечение отвечает требованиям по предельным размерам сварного элемента при сварке сварочной головкой А-639, стр. 148 Учебника (рис. 4.19).

Проверка устойчивости полки.

По табл. 29 СНиП устойчивость полки обеспечена:

.

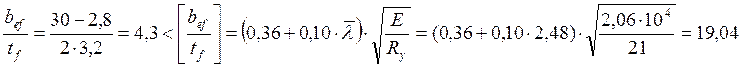Геометрические характеристики сечения:

площадь поперечного сечения:       

А = 2×3,2×30,0 + 2,8×38,6 = 300,08 см²; момент инерции сечения относительно оси х-х:

;

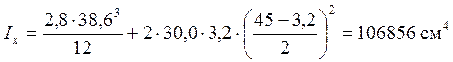момент инерции сечения относительно оси у-у:

;

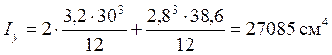радиус инерции сечения относительно оси х-х:

;

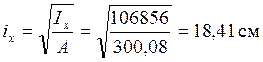радиус инерции сечения относительно оси у-у:

;

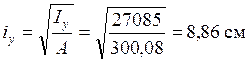момент сопротивления:

;

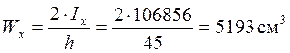ядровое расстояние:

.

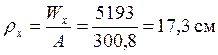Гибкости стержня верхней части колонны:

;                      

;

;

.

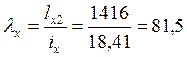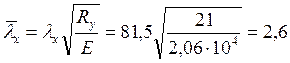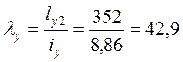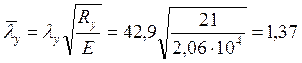По табл. 27 СНиП II-23-81* предельная условная гибкость стенки двутаврового сечения (при т > 1 и условной гибкости ) определяется как

.

Так как переход стенки в критическое состояние еще не означает потерю несущей способности стержня, нормы допускают использование закритической работы стенки. В этом случае часть стенки считают выключившийся из работы и в расчетное сечение колонны включают в запас устойчивости два крайних участка стеки шириной

.

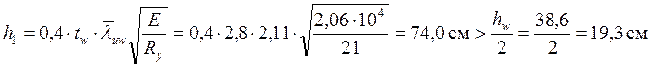Можно утверждать, что стенка не теряет устойчивости, т.к. вся стенка продолжает работать.

Соответствующая площадь сечения:

A_red = 300,08 см².

V.2.1.2. Проверка устойчивости в плоскости действия момента.

Относительный эксцентриситет:

.

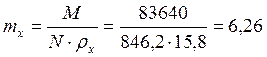Отношение площадей полки и стенки:

.

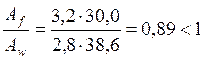Коэффициент влияния формы сечения h.

По табл. 73 СНиП II-23-81* :

 = 1,4 – 0,02×2,6 = 1,35

Приведенный относительный эксцентриситет:

m_ef = h×m_x = 1,35×6,26 = 8,45.

По табл. 74 СНиП II-23-81 находим, что коэффициент j_е = 0,136.

Проверка устойчивости:

.

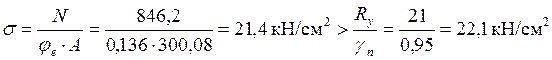Получено небольшое недонапряжение в пределах 3%, что можно считать допустимым.

V.2.1.3.  Проверка устойчивости из плоскости действия момента.

Основное условие:

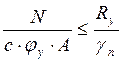, где

j_у – коэффициент устойчивости (по табл. 72 СНиП, при l_у = 42,9, j_у= 0,882);

с – коэффициент, учитывающий влияние момента М_х при изгибно-крутильной форме потере устойчивости.

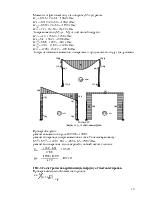
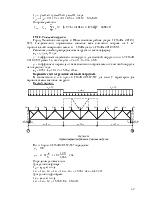
Для определения т_х найдем максимальный момент в средней трети расчетной длины стержня при сочетании нагрузок 1, 2, 3*, 4, 5*: М₁ = -836,4 кНм; М₂ = -507,7 кНм.

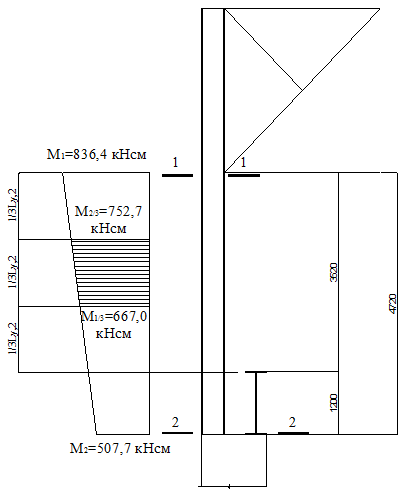
Рисунок 60.

К определению расчетного момента М_х.

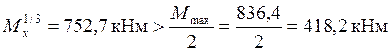, тогда

.

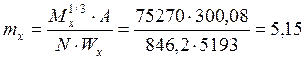Определим коэффициент с:

при 5 < т_х < 10:

с = с₅×(2 – 0,2×m_x) + с₁₀×(0,2×m_x – 1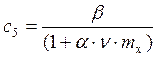), где

, где

a, b, n - коэффициенты, определяемые по прил. 12 учебника;

m_x принимаем равным 5.

При 1 < m_x £ 5

a = 0,65 + 0,05´ m_x = 0,65 + 0,05´5,00 = 0,9.

При`l < 3,14, b = 1.

.

.

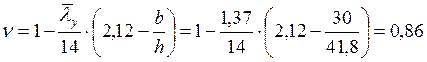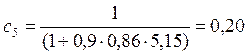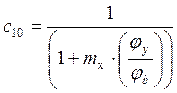, где

j_b – коэффициент снижения расчетного сопротивления при потере устойчивости балок, в большинстве практических случаев при проверке устойчивости колонн принимаемый равным 1;

m_x принимаем равным 10.

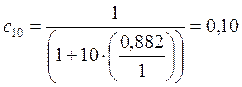
Тогда

с = 0,20×(2 – 0,2×5,15) + 0,1×(0,2×5,15 – 1) = 0,197.

В запас несущей способности в расчет включаем редуцированную площадь A_red:

.

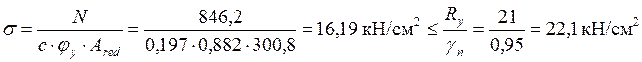Так как m_ef < 20 и верхняя часть колонны не имеет ослабления сечения, то проверку несущей способности колонны делать нет необходимости.

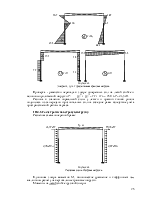
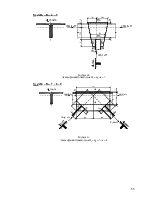
V.2.2. Подбор сечения нижней части колонны.

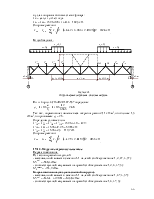
Подберем несимметричное сечение стержня: подкрановая ветвь из прокатного двутавра, остальная часть из сварных стальных листов.

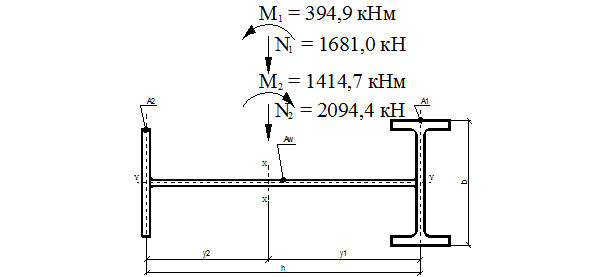
Рисунок 61.

К подбору сечения несимметричной формы.

Высота сечения нижней части колонны принята h = 1000 мм.

Расчетные усилия в нижней части колонны:

N₃ = -1681,0 кН; М₃ = -394,9 кНм (изгибающий момент догружает наружную полку);

N₄ = -2094,4 кН; М₄ = 1414,7 кНм (изгибающий момент догружает подкрановую полку);

Q_max = 124,7 кН.

Введем следующие безразмерные параметры:

показатель асимметрии:

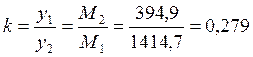, тогда

;

.

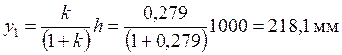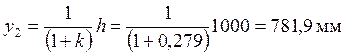Характеристика распределения материала в сечении p = A_w/A » 0,4.

Геометрические характеристики сечения:

Момент инерции относительно оси х – х:

;

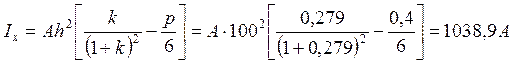Площадь стенки сечения:

A_w = p×A = 0,4А;

Радиус инерции сечения относительно оси х – х:

;

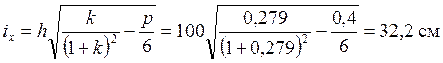Ядровые расстояния:

r_x1 = i_x²/y₁ = 32,2²/21,81 = 47,5 см;

r_x2 = i_x²/y₂ = 32,2²/78,19 = 13,3 см;

Условная гибкость нижней части колонны в плоскости рамы:

.

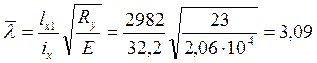Относительный эксцентриситет:

.

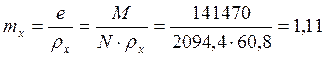По табл. 73 СНиП II-23-81 находим, что коэффициент влияния формы сечения в первом приближении:

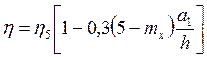, где

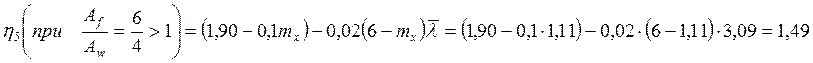
в первом приближении принимаем 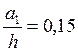, тогда

.

Приведенный относительный эксцентриситет:

m_ef = h×m_x = 1,23×1,11 = 1,37.

По табл. 74 СНиП II-23-81 находим, что коэффициент j_е = 0,3729.

Требуемая площадь сечения, определяемая из комбинации с максимальным моментом:

.

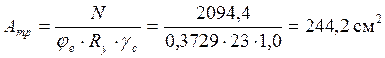V.2.2.1. Компоновка сечения нижней части колонны.

Предварительно принимаем толщину полки t_f = 16 мм, тогда высота стенки:

h_w = h – 2×t = 100 – 2×1,6 = 96,8 см.

Требуемая толщина стенки подбирается из условия ее местной устойчивости.

По табл. 27 СНиП II-23-81* предельная условная гибкость стенки двутаврового сечения (при т > 1 и условной гибкости ) определяется как

, тогда

,

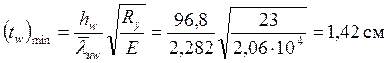Предполагая потерю устойчивости стенки по время работы, принимаем минимальную толщину стенки t_w = 0,8 мм.

Требуемая площадь полок:

(А_f)_тр= А_тр – A_w = 244,2 – 96,8×0,8 = 166,8 см².

Распределим площадь по двум полкам пропорционально моментам приходящимся на них:

наружная полка:         ;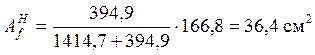

внутренняя полка:      А_f^B = 166,8 – 36,4 = 130,4 см².

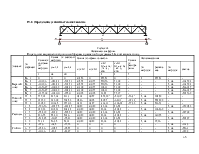
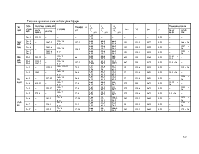
Принимаем для внутренней полки широкополочный двутавр 40Ш2:

Найдем толщину наружной полки, принимая примерно равной ее ширину