Теплообмен и конструирование электронной аппаратуры: Методическое руководство к курсовой работе, страница 6

Определение  и  требует отдельного рассмотрения.

3. Определение теплового коэффициента

Определение структуры  базируется на представлении нагретой зоны в виде однородного анизотропного параллелепипеда с равномерно распределенными источниками тепла.

Переход от системы разнородных тел, каковой является в действительности нагретая зона, к однородному телу и вычисление эффективных коэффициентов теплопроводности , ,  в направлении , ,  приводится в разделе VII.

Температурное поле анизотропного параллелепипеда с внутренними источниками тепла описывается дифференциальным уравнением теплопроводности

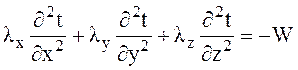
с граничными условиями первого рода

, где , ,  – текущие координаты, отсчитываемые от одного из узлов параллелепипеда;

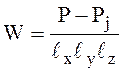 – объемная плотность источников тепла;

, ,  – размеры нагретой зоны.

Совместное решение уравнения теплопроводности и уравнения для граничных условий позволяет найти структуру .

Для центральной точки параллелепипеда (нагретой зоны) тепловой коэффициент  будет максимальным и равным

;

где коэффициент 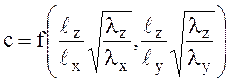 определяется по графикам на рис. 4. При расчете изводится так, чтобы выполнялись соотношения

; .

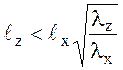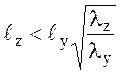Для любой другой точки нагретой зоны тепловой коэффициент

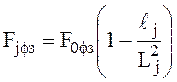, где  – расстояние от центра нагретой зоны до точки ;

 – расстояние от центра нагретой зоны до его поверхности по прямой, проходящей через точку .

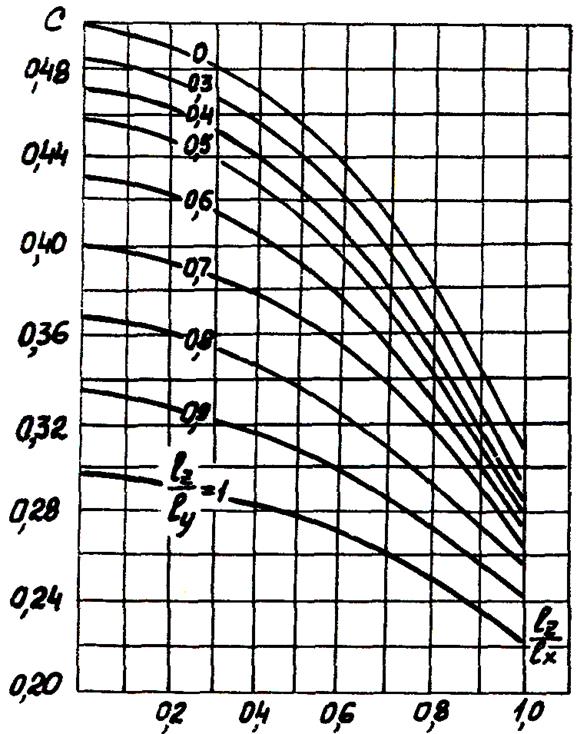
Рис. 4

4. Определение теплового сопротивления

 представляет собой тепловое сопротивление прямоугольной оболочки, которое преодолевается тепловым потоком  при переменной площади сечения, перпендикулярной направлению теплового потока.

Внутренней поверхностью такой оболочки является функциональный узел (модуль), внешней поверхностью – нагретая зона, причем центры их в общем случае не совпадают.

Для расчета используем формулу для определения тепловой проводимости такой оболочки:

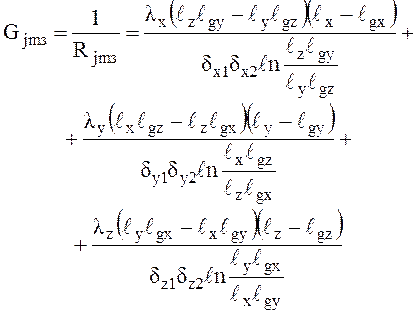
где                 , ,  – размеры функционального узла в направлениях , , ;

, , , , ,  – расстояния между функциональным узлом и поверхностью нагретой зоны в направлениях , , ;

Принято, что начало координат расположено в одном из углов нагретой зоны.

VII. ОПРЕДЕЛЕНИЕ ЭФФЕКТИВНЫХ КОЭФФИЦИЕНТОВ ТЕПЛОПРОВОДНОСТИ

Определение эффективных коэффициентов теплопроводности , ,  нагретой зоны (или другой области) связано с определением тепловых проводимостей , ,  в направлениях

; ;

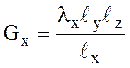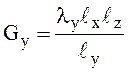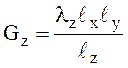
или

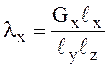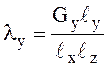; ; , где , ,  – размеры нагретой зоны в направлениях , , .

Для определения , ,  необходимо:

1) разбить нагретую зону на прямоугольные ячейки с учетом ее конструктивных особенностей и характера размещения функциональных узлов;

2) определить для каждой ячейки тепловые проводимости , , ;

3) суммировать тепловые проводимости ячеек с учетом их последовательно-параллельного размещения в нагретой зоне.

В общем случае такая ячейка включает следущие элементы: функциональный узел, элемент установочной (печатной) платы и окружающие функциональный узел газообразные, жидкие или твердые прослойки. Могут быть и другие варианты.

Перенос тепла через элементы ячейки в направлениях , ,  рассматривается как перенос через твердые плоские стенки, в которых поверхности, перпендикулярные направлению потока, изотермичны, а параллельные – адиабатические.

Например, ячейка на рис.5,а состоит из четырех элементов: 1 – элемент установочной платы; 2 – функциональный узел; 3 – зазор воздушный между функциональным узлом и следующей ячейкой в направлении ; 4 – воздушный зазор между функциональными узлами в направлении .

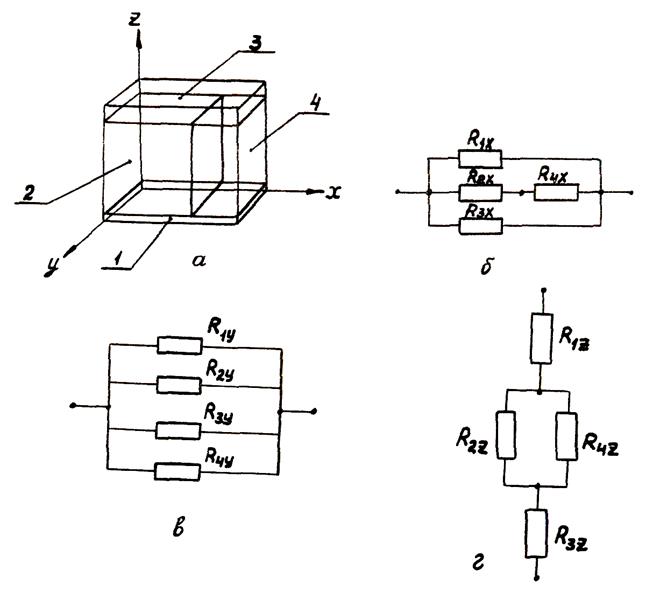
Рис. 5

Зная геометрические размеры и коэффициенты теплопроводности элементов ячейки,нетрудно определить тепловые проводимости ячейки , ,  (рис.5 б, в, г):

;

;

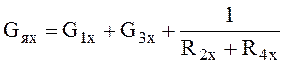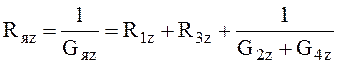, где , ,  – тепловые проводимости элементов ячейки; .

VIII. ОПРЕДЕЛЕНИЕ ТЕМПЕРАТУРНОГО ПОЛЯ МИКРОСХЕМ АНАЛИТИЧЕСКИМ МЕТОДОМ С ПОМОЩЬЮ ЭВМ