Исследование эффективности алгоритмов размещения конструктивных элементов РЭС

Ульяновский государственный технический университет

Лабораторная работа №3

ИССЛЕДОВАНИЕ  ЭФФЕКТИВНОСТИ  АЛГОРИТМОВ

РАЗМЕЩЕНИЯ  КОНСТРУКТИВНЫХ  ЭЛЕМЕНТОВ  РЭС

Выполнил:                                                                        Проверил:

Студент гр. Рз-41                                                             преподаватель

Халитов Р.Г.                                                      Мактас М.Я.        

Ульяновск 2005

Цель работы: исследовать эффективность алгоритмов размещения элементов РЭС в коммутационном пространстве, освоить особенности алгоритмизации и программирования задачи размещения на ПЭВМ, приобрести навыки построения математических моделей монтажного пространства и схем соединения модулей, реализации и исследования их при решении задачи размещения с применением  САПР.

1. ОСНОВНЫЕ МЕТОДЫ ОЦЕНКИ ЭФФЕКТИВНОСТИ

АЛГОРИТМОВ РАЗМЕЩЕНИЯ

При разработке алгоритмов и программ следует стремиться к наиболее полному удовлетворению требований, предъявляемых к ним: минимальная продолжительность решения, максимальный объем задач при заданной емкости оперативной емкости ЭВМ, максимальная точность решения, высокая надёжность, эффективность, завершённость, понятность и т.д.

Перечисленные показатели определяют качество программного обеспечения САПР. Причём на этапе разработки алгоритмов достаточно учесть такие показатели, как точность, временная и емкостная сложность, а при разработке программ или их сравнении следует учитывать и остальные показатели [1 – 4].

Объективная оценка эффективности алгоритмов размещения должна опираться на анализ точности решений и времени их получения в зависимости от основных параметров задачи.

Для оценки качества решения рекомендуются два подхода [1]:

1  применение тест – задач;

2  статистическая обработка результатов.

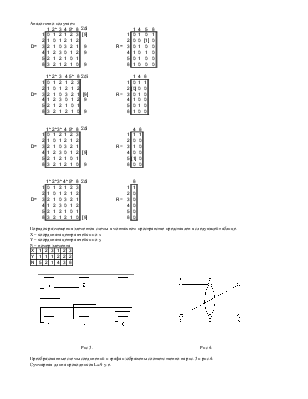
Первый способ заключается в том, что каким-либо образом находят точное (глобально – оптимальное) решение F_opt некоторого варианта W задачи Z. Затем этот вариант W решают с помощью алгоритмов А₁, А₂,…, А_n и анализируют, насколько i–й (i =`1, n) результат отличается от F_opt. Например, алгоритмы размещения равногабаритных элементов по критерию минимума суммарной длины соединений могут сравниваться по результатам решения тест-задачи Штейнберга. В ней предлагается на 36 заданных позиций разместить 34 элемента, матрица связности для которых также известна. Тот алгоритм, который даст размещение с меньшей суммарной длиной соединений, и будет считаться лучшим.

При рассмотрении этих результатов надо учитывать, что машинное время в значительной мере зависит от характеристик ЭВМ и тщательности программирования. Кроме того, сопоставление алгоритмов на одном или нескольких примерах не может дать достоверной информации об эффективности алгоритма.

Второй– статистический способ оценки качества решения состоит в том, что формируется m вариантов задачи Z. Решив эти варианты с помощью алгоритмов А₁, А₂, …, А_n, получают n результатов R_i (i=1, n`), которые оценивается рядом показателей P = {P₁, P₂, …, P_n} и выполняют их статистическую обработку и сравнение. Такой подход позволяет получить наиболее объективные результаты для оценки качества приближенных алгоритмов.

Другими словами, для оценки алгоритма размещения надо решить этим алгоритмом m задач и определить среднюю суммарную длину соединений, полученных размещений. Затем это же множество задач m решить другим алгоритмом и выполнить такую же оценку. Лучшим будет тот из алгоритмов, который даст меньшую среднюю суммарную длину соединений.

2.  ОБЩИЕ СВЕДЕНИЯ О ЗАДАЧЕ РАЗМЕЩЕНИЯ

После распределения конструктивных элементов РЭС по коммутационным пространствам различного уровня иерархии, для каждой полученной в результате компоновки сборочной единицы производят размещение включенных в ее состав элементов предыдущего уровня, т.е. выбирают такое их взаимное расположение, при котором наилучшим образом учитываются предъявляемые к аппаратуре требования [1 – 3, 7 11].

Исходными данными для решения задачи размещения являются:

-   данные о конфигурации и размерах коммутационного пространства, определяемые требованиями установки и крепления соответствующей сборочной единицы в аппаратуре;

-   количество и геометрические размеры конструктивных элементов, подлежащих размещению;

-   схема соединений, а также ряд ограничений на взаимное расположение отдельных элементов, учитывающих особенности разрабатываемой  конструкции.

Задача сводится к отысканию для каждого размещаемого элемента таких позиций, при которых оптимизируется выбранный показатель качества L, и обеспечиваются наиболее благоприятные условия для последующего электрического монтажа.

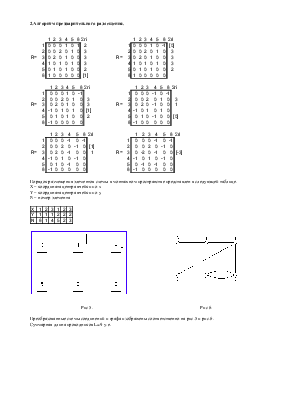
В том случае, если в качестве критерия размещения используют минимум суммарной взвешенной длины соединений, необходимо сформировать матрицу расстояний размещённых элементов  P = || p_ij ||_n*m .

Здесь P_ij = |x_i - x_j| + |y_i - y_j|, а  x_i, x_j  и y_i, y_j  – координаты позиций, в которые размещены соответственно i–й и j–й модули.

Тогда суммарная взвешенная длина соединений будет равна где r_ij – элемент матрицы связности R, а p_ij  – элемент матрицы размещения P.

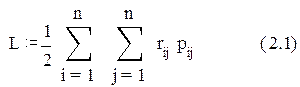Математически задача формулируется следующим образом [1 - 5]. Электрическая схема представляется в виде мультиграфа, а моделью монтажного пространства служит графовая решётка. Требуется вершины мультиграфа разместить в узлы графовой решётки таким образом, чтобы суммарная длина ребер размещенного мультиграфа была минимальна.

Задача размещения является комбинаторной, т.е. может быть решена только полным перебором (для размещения n элементов на n позиций существует n! вариантов размещения). Для решения задач размещения разработано большое количество различных алгоритмов [1 – 4]. В данной работе рассмотрим эвристические алгоритмы